
20. (本题满分16分)已知函数 ,
,
(1) 讨论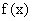 的单调性;
的单调性;
(2) 设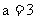 , 求
, 求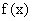 在区间
在区间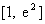 上值域. 期中
上值域. 期中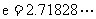 是自然对数的底数.
是自然对数的底数.
19. (本题满分16分)在平面直角坐标系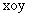 中, 已知圆心在第二象限、半径为
中, 已知圆心在第二象限、半径为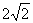 的圆
的圆
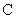 与直线
与直线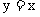 相切于坐标原点
相切于坐标原点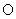 . 椭圆
. 椭圆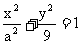 与圆
与圆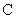 的一个交点到椭圆两焦点的
的一个交点到椭圆两焦点的
距离之和为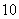 . (1) 求圆
. (1) 求圆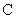 的方程;
的方程;
(2) 试探究圆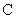 上是否存在异于原点的点
上是否存在异于原点的点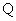 ,使
,使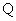 到椭圆右焦点
到椭圆右焦点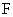 的距离等于线段
的距离等于线段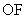 的长.
的长.
若存在, 请求出点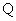 的坐标; 若不存在, 请说明理由.
的坐标; 若不存在, 请说明理由.
18. (本题满分16分)2010年上海世博会某国要建一座八边形的展馆区, 它的主体造型的平面
图是由二个相同的矩形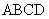 和
和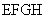 构成的面积为
构成的面积为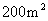 的十字型地域, 计划在正方形
的十字型地域, 计划在正方形
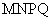 上建一座“观景花坛”, 造价为
上建一座“观景花坛”, 造价为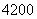 元/
元/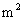 , 在四个相同的矩形上(图中阴影部分)
, 在四个相同的矩形上(图中阴影部分)
铺花岗岩地坪, 造价为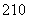 元/
元/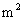 , 再在四个空角(如
, 再在四个空角(如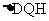 等)上铺草坪, 造价为
等)上铺草坪, 造价为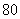 元/
元/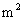 .
.
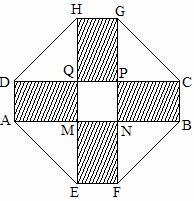 (1) 设总造价为
(1) 设总造价为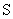 元,
元, 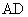 长为
长为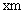 , 试建立
, 试建立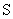 与
与 的函数关系;
的函数关系;
(2) 当 为何值时, S最小?并求这个最小值.
为何值时, S最小?并求这个最小值.
17. (本题满分14分)已知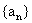 是各项均为正数的等差数列,
是各项均为正数的等差数列, 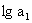 、
、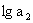 、
、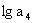 成等差数列.
成等差数列.
又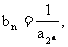
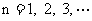 . (1)
证明
. (1)
证明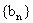 为等比数列;
为等比数列;
(2) 如果数列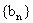 前3项的和等于
前3项的和等于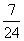 , 求数列
, 求数列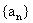 的首项
的首项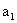 和公差
和公差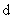 .
.
16.
(本题满分14分)已知正方体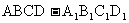 中,
中, 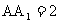 ,
, 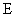 为棱
为棱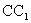 的中点.
的中点.
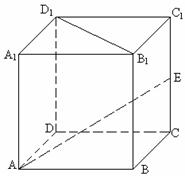 (1) 求证
(1) 求证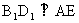 ; (2) 求证
; (2) 求证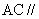 平面
平面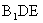 ;
;
(3) 求三棱锥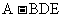 体积.
体积.
15. (本题满分14分)在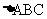 中, 角
中, 角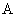 ,
,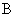 ,
,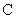 的对边分别
的对边分别
为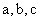 , 已知向量
, 已知向量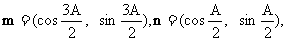 且满足
且满足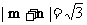 ,
,
(1) 求角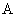 的大小; (2) 若
的大小; (2) 若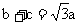 , 试判断
, 试判断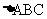 的形状.
的形状.
14.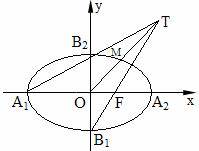 如图, 在平面直角坐标系
如图, 在平面直角坐标系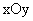 中,
中, 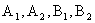 为椭圆
为椭圆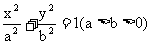 的四个
的四个
顶点, 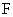 为其右焦点, 直线
为其右焦点, 直线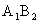 与直线
与直线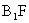 相交于点
相交于点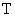 ,
,
线段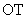 与椭圆的交点
与椭圆的交点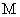 恰为线段
恰为线段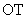 的中点, 则该
的中点, 则该
椭圆的离心率为 .
13. 设正数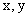 满足
满足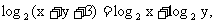 则
则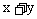 的取值范围是
.
的取值范围是
.
12. 已知平面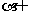 平面
平面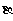
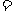 l, 异于直线l的直线
l, 异于直线l的直线 , 异于直线l的直线
, 异于直线l的直线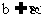 , 且
, 且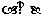 ,
,
命题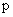 :
: 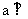 l, 命题
l, 命题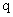 :
: 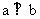 则
则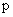 是
是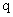 的
. (填写正确的序号)
的
. (填写正确的序号)
① 充分而不必要条件 ② 必要而不充分条件
③ 充要条件 ④ 既不充分又不必要条件
11. 不等式组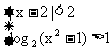 的解集为
.
的解集为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com