
2.用计算器求值(保留4位有效数字)
(1) (2)
(2)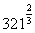 (3)
(3)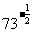
(4)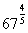 (5)
(5)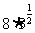 (6)25·
(6)25·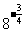
解:(1) =1.710 (2)
=1.710 (2) 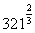 =46.88
=46.88
(3)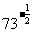 =0.1170 (4)
=0.1170 (4) 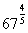 =28.90
=28.90
(5)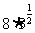 =2.881 (6)25·
=2.881 (6)25·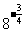 =0.08735
=0.08735
1.课本P75习题2.5
分数指数幂的意义,分数指数幂与根式的互化,有理指数幂的运算性质.
2.用分数指数幂表示下列各式:
(1)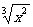 (2)
(2)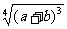 (a+b>0)
(a+b>0)
(3) (4)
(4) (m>n)
(m>n)
(5)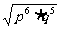 (p>0) (6)
(p>0) (6)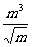
解:(1) 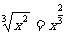
(2) 
(3) 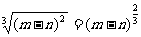
(4) 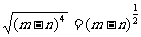 =(m-n)2
=(m-n)2
(5) 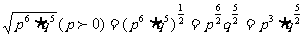
(6) 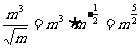
1.用根式的形式表示下列各式(a>0)
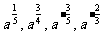
解: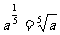
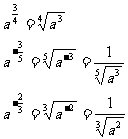
例1求值: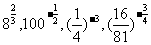 .
.
解: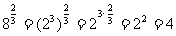

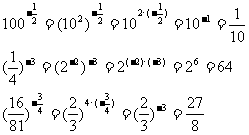

例2用分数指数幂的形式表示下列各式:
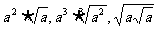 (式中a>0)
(式中a>0) 
解: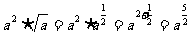

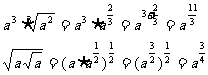

例3计算下列各式(式中字母都是正数)
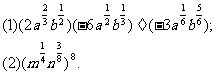
分析:(1)题可以仿照单项式乘除法进行,首先是系数相乘除,然后是同底数幂相乘除,并且要注意符号
(2)题按积的乘方计算,而按幂的乘方计算,等熟练后可简化计算步骤
解
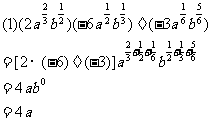
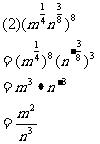
例4计算下列各式:
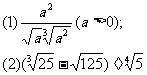
分析:(1)题把根式化成分数指数幂的形式,再计算
(2)题先把根式化成分数指数幂的最简形式,然后计算
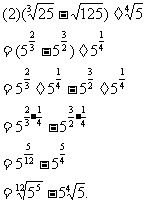
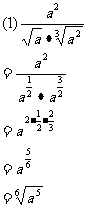 解:
解:
3.有理指数幂的运算性质:
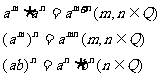

说明:若a>0,P是一个无理数,则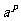 表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用,有关概念和证明在本书从略.?
表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用,有关概念和证明在本书从略.?
2.规定:
(1)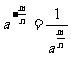 (a>0,m,n∈N*,且n>1)
(a>0,m,n∈N*,且n>1) 
(2)0的正分数指数幂等于0.
(3)0的负分数指数幂无意义.
规定了分数指数幂的意义以后,指数的概念就从整数推广到有理数指数.当a>0时,整数指数幂的运算性质,对于有理指数幂也同样适用.即对于任意有理数r,s,均有下面的运算性质.
1.正数的正分数指数幂的意义
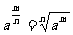 (a>0,m,n∈N*,且n>1)
(a>0,m,n∈N*,且n>1) 
要注意两点:一是分数指数幂是根式的另一种表示形式;二是根式与分数指数幂可以进行互化.
另外,我们还要对正数的负分数指数幂和0的分数指数幂作如下规定.
3.引例:当a>0时
①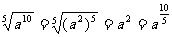

②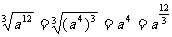

③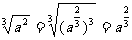

④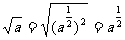

上述推导过程主要利用了根式的运算性质,例子③、④、⑤用到了推广的整数指数幂运算性质(2).因此,我们可以得出正分数指数幂的意义.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com