
2. 掌握碳及其化合物的重要性质。
1. 了解碳族元素性质及其递变规律,学会运用元素周期律的知识指导碳族元素及其化合物的学习。
1 若
若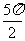 ≤α≤
≤α≤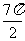 ,则
,则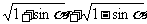 等于( )
等于( )
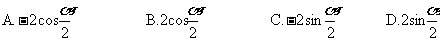
2
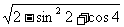 的值等于( )
的值等于( )
A sin2
B
sin2
B -cos2
C
-cos2
C
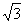 cos2 D
cos2 D -
-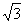 cos2
cos2
3 sin6°cos24°sin78°cos48°的值为( )
sin6°cos24°sin78°cos48°的值为( )

4
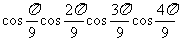 的值等于
的值等于 
5 已知sinx=
已知sinx=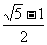 ,则sin2(x-
,则sin2(x-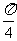 )的值等于
)的值等于

6 若sinαsinβ+cosαcosβ=0,则sinαcosα+sinβcosβ的值为
若sinαsinβ+cosαcosβ=0,则sinαcosα+sinβcosβ的值为 
7 已知
已知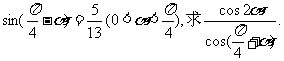
8 求值tan70°cos10°(
求值tan70°cos10°(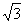 tan20°-1)
tan20°-1)
1 求值:cos280°+sin250°-sin190°·cos320°
求值:cos280°+sin250°-sin190°·cos320°
解:原式=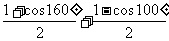 +sin10°cos40°
+sin10°cos40°
=1+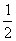 ×2×(-sin30°sin50°)+sin10°cos40°
×2×(-sin30°sin50°)+sin10°cos40°
=1-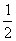 sin50°+
sin50°+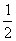 (sin50°-sin30°)
(sin50°-sin30°)
=1-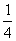 =
=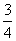
2 求
求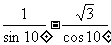 的值
的值
解:原式=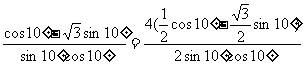
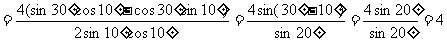
5.cos20°cos40°cos80° = 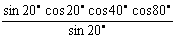
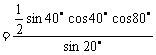

例2求证:[sinq(1+sinq)+cosq(1+cosq)]×[sinq(1-sinq)+cosq(1-cosq)] = sin2q
证:左边 = (sinq+sin2q+cosq+cos2q)×(sinq-sin2q+cosq-cos2q)
= (sinq+ cosq+1)×(sinq+cosq -1)
= (sinq+ cosq)2 -1 = 2sinqcosq = sin2q = 右边
∴原式得证
关于“升幂”“降次”的应用:在二倍角公式中,“升次”“降次”与角的变化是相对的 在解题中应视题目的具体情况灵活掌握应用
在解题中应视题目的具体情况灵活掌握应用
例3求函数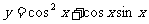 的值域
的值域
解: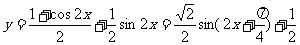 --降次
--降次
∵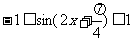 ∴
∴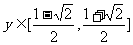
例4 求证: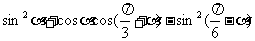 的值是与a无关的定值
的值是与a无关的定值 证:
证: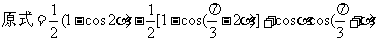 -降次
-降次
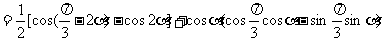
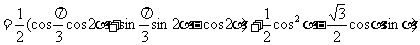
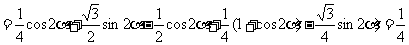
∴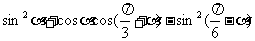 的值与a无关
的值与a无关
例5 化简: --升幂
--升幂
解: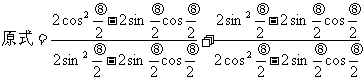
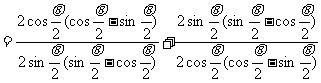

例6 求证: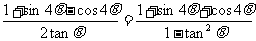 --升幂
--升幂
证:原式等价于: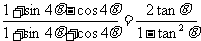
左边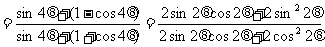
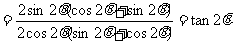
右边=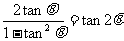
∴左边=右边 ∴原式得证
例7利用三角公式化简: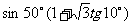
分析:化正切为正弦、余弦,便于探索解题思路.
解: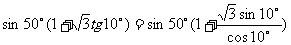
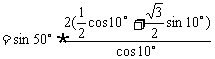
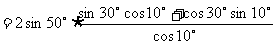
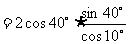
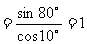
指出:例4的解法用到了很多公式,其解法的关键是“化切为弦”与逆用公式.
4.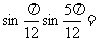
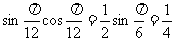
3.2sin2157 5° - 1 =
5° - 1 = 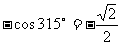
2.
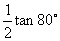
例1化简下列各式:
1.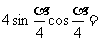
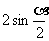
二倍角公式:
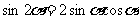 ;
;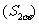
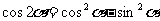 ;
;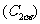
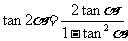 ;
;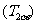
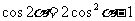
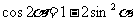

(1)二倍角公式的作用在于用单角的三角函数来表达二倍角的三角函数,它适用于二倍角与单角的三角函数之间的互化问题.
(2)二倍角公式为仅限于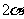 是
是 的二倍的形式,尤其是“倍角”的意义是相对的
的二倍的形式,尤其是“倍角”的意义是相对的
(3)二倍角公式是从两角和的三角函数公式中,取两角相等时推导出,记忆时可联想相应角的公式.
(4) 公式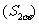 ,
,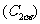 ,
, ,
,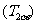 成立的条件是: 公式
成立的条件是: 公式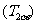 成立的条件是
成立的条件是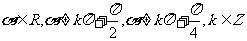 .其他
.其他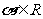

(5)熟悉“倍角”与“二次”的关系(升角-降次,降角-升次)
(6)特别注意公式的三角表达形式,且要善于变形:
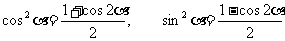 这两个形式今后常用
这两个形式今后常用
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com