
2.下列句子中,没有语病的一句是
A.昨日,已逝女台湾作家林海音的追思会在台北举行。
B.美国国防部发言人4月7日称,美英联军已向巴格达派遣了数百辆坦克、装甲车和军用车辆。
C.要不要打击恐怖主义?在打击恐怖主义的时候,能不能不侵犯他国主权?对这两个问题我国政府表明了自己的立场。
D.四月八日,湖南高校学术考察团一行十三人在美国宾夕法尼亚州中部地区发生车祸,目前还没有伤亡的人员报告。
1.下列各句中,没有语病的一句是
A.这次网络短训班的学员,除北大本校人员外,还有来自清华大学等15所高校的教师、学生和科技工作者也参加了学习。
B.我们的报刊、杂志、电视和一切出版物,更有责任作出表率,杜绝用字不规范的现象,增强使用语言文字的规范意识。
C.在新的千年里,中华民族这条巨龙一定会昂首腾飞于无垠的天际,创造出令世界惊异的奇迹来。
D.这家工厂虽然规模不大,但曾两次荣获省科学大会奖,三次被授予省优质产品称号,产品远销全国各地和东南亚地区。
(18)(本题满分14分)在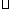 ABC中,角A、B、C所对应的边分别为a、b、c,且满足
ABC中,角A、B、C所对应的边分别为a、b、c,且满足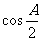 =
=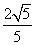 ,
,
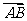
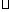
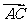 =3.
=3.
(Ⅰ)求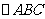 的面积;
的面积; 

(Ⅱ)若b+c=6,求a的值。
(19)(本题满分14分)在1,2,3…,9,这9个自然数中,任取3个数.
(Ⅰ)求这3个数中,恰有一个是偶数的概率; 

(Ⅱ)记ξ为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时ξ的值是2)。求随机变量ξ的分布列及其数学期望Eξ.
(20)(本题满分15分)如图,平面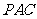 ⊥平面
⊥平面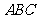 ,
,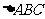 是以
是以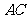 为斜边的等腰直角三角形。
为斜边的等腰直角三角形。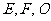 分别为
分别为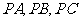 的中点,
的中点,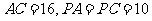 。
。
(I) 设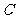 是
是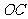 的中点,证明:
的中点,证明: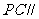 平面
平面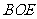 ;
; 

(II)证明:在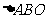 内存在一点
内存在一点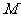 ,使
,使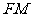 ⊥平面
⊥平面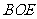 ,并求点
,并求点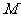 到
到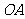 ,
,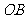 的距离。
的距离。
(21)(本题满分15分)已知椭圆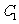 :
: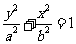 (
(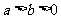 )的右顶点
)的右顶点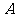 (1,0),过
(1,0),过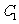 的焦点且垂直长轴的弦长为1。
的焦点且垂直长轴的弦长为1。 

(I) 求椭圆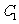 的方程;
的方程;
(II) 设点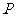 在抛物线
在抛物线 :
: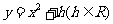 上,
上, 在点P处的切线与
在点P处的切线与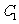 交于点
交于点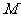 ,
, 。当线段AP的中点与MN的中点的横坐标相等时,求
。当线段AP的中点与MN的中点的横坐标相等时,求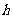 的最小值。
的最小值。
(22)(本题满分14分)已知函数 ,
,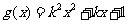 ,其中
,其中 。
。
(I) 设函数 。若
。若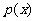


(II)设函数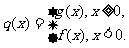 是否存在
是否存在 ,对任意给定的非零实数
,对任意给定的非零实数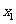 ,存在惟一的非零实数
,存在惟一的非零实数 (
(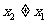 ),使得
),使得 ?若存在,求
?若存在,求 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(11)设等比数列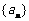 的公比
的公比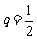 ,前n项和为
,前n项和为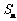 ,
,
则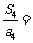 _____________.
_____________.


(12)若某几何体的三视图(单元:cm)如图所示,则
此几何体的体积是________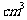 .
.
(13)若实数x,y满足不等式组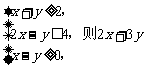
的最小值是__________.
(14)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:
|
高峰时间段用电价格表 |
|
低谷时间段用电价格表 |
||
|
高峰月用电量 (单位:千瓦时) |
高峰电价 (单位:元/千瓦时) |
|
低谷月用电量 (单位:千瓦时) |
低谷电价 (单位:元/千瓦时) |
|
50及以下的部分 |
0.568 |
|
50及以下的部分 |
0.288 |
|
超过50至200的部分 |
0.598 |
|
超过50至200的部分 |
0.318 |
|
超过200的部分 |
0.668 |
|
超过200的部分 |
0.388 |
若某家庭5月份的高峰时间用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________元(用数字作答)。
观察下列等式:
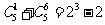 ,
,
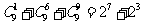 ,
,
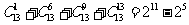 ,
,
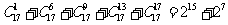 ,
,
……
由以上等式推测到一个一般的结论:
对于n∈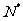 ,
, _________.
_________. 

(16)甲、乙、丙三人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是________(用数字作答)
(17)如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将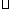 AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.
AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.
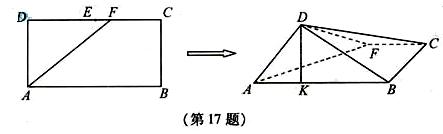
(1)
设U=R,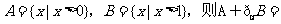
(A)
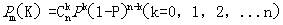 (B)
(B)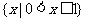 (C)
(C)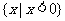 (D)
(D)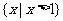
(2)已知a、b是实数,则“a>0,b>0”是a+b>0且ab>0的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(3)设z=1+i(i是虚数单位),则
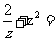
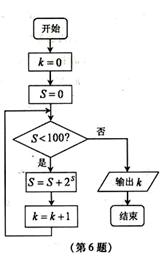 (A)-1-i (B)-1+ i (C)1- i (D)1+i
(A)-1-i (B)-1+ i (C)1- i (D)1+i
(4)在二项式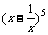 的展开式中,含x4的项的系数是
的展开式中,含x4的项的系数是
(A)-10 (B)10
(C)-5 (D)5
(5)在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D式侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是
(A)300 (B)450
(C)600 (D)900
(6)某程序框图如图所示,该程序运行后输出的k的值是
(A)4 (B)5 (C)6 (D)7 

(7)设向量a,b满足︱a︱=3,︱b︱=4,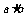 =0.以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为
=0.以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为
(A)3 (B)4 (C)5 (D)6
(8)已知a是实数,则函数f(x)=1+asinax的图像不可能是

(9)过双曲线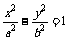 (a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若
(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若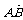 =
= ,则双曲线的离心率是
,则双曲线的离心率是 

(A)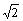 (B)
(B)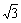 (C)
(C)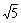 (D)
(D)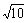
(10)对于正实数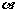 ,记M
,记M 为满足下述条件的函数f(x)构成的集合:
为满足下述条件的函数f(x)构成的集合: 且
且 >
>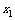 ,有-
,有-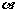 (
( -
-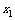 )<f(
)<f( )-f(
)-f(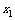 )<
)<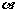 (
( -
-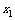 ).下列结论正确的是
).下列结论正确的是
(A)若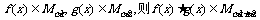
(B)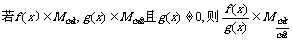
(C)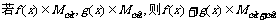


(D)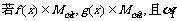 >
>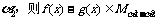
2009年普通高等学校招生全国统一考试
数学(理科)
非选择题部分(共100分)
(17)(本小题满分12分)
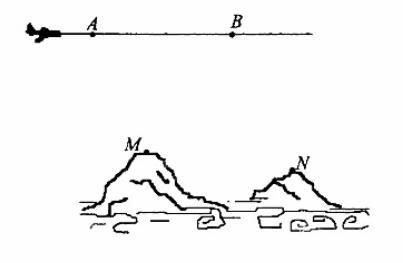
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。
(18)(本小题满分12分)
某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人; 

(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.

(i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论) 

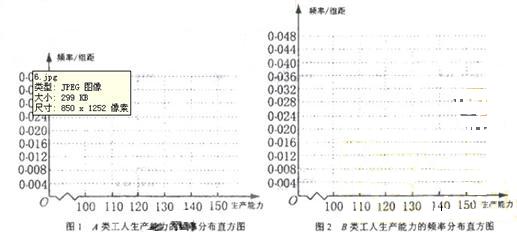
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表) 

(19)(本小题满分12分)
 如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的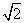 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD; 

(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 

使得BE∥平面PAC。若存在,求SE:EC的值;
若不存在,试说明理由。
(20)(本小题满分12分)
已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,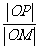 =λ,求点M的轨迹方程,并说明轨迹是什么曲线。
=λ,求点M的轨迹方程,并说明轨迹是什么曲线。 

(21)(本小题满分12分)
已知函数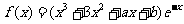
(I)
如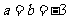 ,求
,求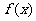 的单调区间;
的单调区间;
(II)
若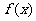 在
在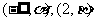 单调增加,在
单调增加,在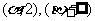 单调减少,证明
单调减少,证明
 <6.
<6. 

请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
(22)本小题满分10分)选修4-1:几何证明选讲 

如图,已知 的两条角平分线
的两条角平分线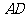 和
和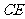 相交于H,
相交于H,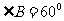 ,F在
,F在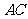 上,
上,
且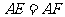 。
。
(I) 证明:B,D,H,E四点共圆:
(II)
证明: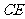 平分
平分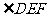 。
。 

(23)(本小题满分10分)选修4-4:坐标系于参数方程
已知曲线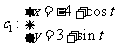 (t为参数),
(t为参数), 

(24)(本小题满分10分)选修4-5:不等式选讲
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
(1)将y表示成x的函数;
(2)要使y的值不超过70,x 应该在什么范围内取值? 


(13)设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点。若AB的中点为(2,2),则直线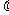 的方程为_____________.
的方程为_____________.
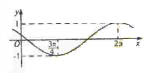 (14)已知函数y=sin(
(14)已知函数y=sin(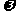 x+
x+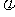 )(
)(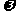 >0, -
>0, -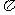

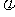 <
<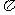 )的图像如图所示,则
)的图像如图所示,则 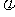 =________________
=________________
(15)7名志愿者中安排6人在周六、周日两天参加社区公益活动。若每天安排3人,则不同的安排方案共有________________种(用数字作答)。
(16)等差数列{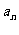 }前n项和为
}前n项和为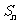 。已知
。已知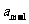 +
+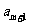 -
-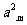 =0,
=0,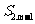 =38,则m=_______
=38,则m=_______
(16)(本小题满分12分)
在△ABC中,sin(C-A)=1,sinB=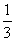 .
.
(Ⅰ)求sinA的值;
(Ⅱ)设AC=,求△ABC的面积.


(17)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区,B肯定是受A感染的。对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是1/2.同样也假设D受A、B和C感染的概率都是1/3.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
(18)(本小题满分13分)
如图,四棱椎F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.
(Ⅰ) 求二面角B-AF-D的大小;
(Ⅱ) 求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积。 

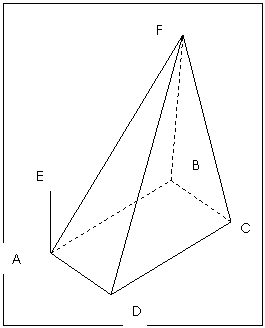
第(18)题图
(19)(本小题满分12分)
已知函数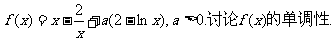


(20)(本小题满分13分)
点P(x0,y0)在椭圆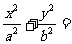 1(a>b>0)上,x0=
1(a>b>0)上,x0=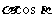 , y0=
, y0=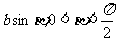 . 直线
. 直线 与直线
与直线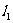 :
: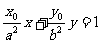 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为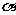 ,直线
,直线 的倾斜角为
的倾斜角为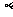 .
.
(Ⅰ)证明:点P是椭圆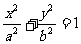 与直线
与直线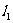 的唯一交点;
的唯一交点;
(Ⅱ)证明:tan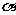 ,tan
,tan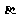 ,tan
,tan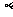 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列{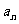 }满足
}满足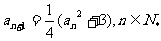 .
.
(Ⅰ)证明:若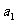 为奇数,则对一切
为奇数,则对一切 ,
,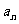 都是奇数;
都是奇数;
(Ⅱ)若对一切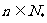 ,都有
,都有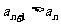 ,求
,求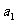 的取值范围。
的取值范围。
W数学(理科)试题 第4页(共4页) 

(11)若随机变量X~N(μ,σ2),则P(X≤μ)= .
(12)以直角坐标系的原点为极点,x轴的正半轴为极轴, 

并在两种坐标系中取相同的长度单位,已知直线的
 极坐标方程为
极坐标方程为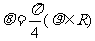 ,它与曲线
,它与曲线
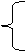

(α为参数)相交于两点A和B,则

|AB|= .
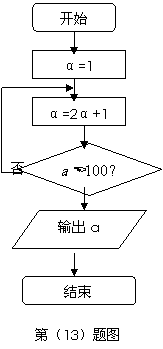
(13)程序框图(即算法流程图)如图所示,其输出结果是
.
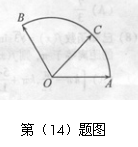
(14)给定两个长度为1的平面向量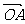 和
和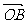 ,它们的夹
,它们的夹
角为120°.如图所示,点C在以O为圆心的圆弧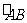
上变动.若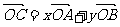 ,其中
,其中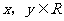 ,则x+y
,则x+y
的最大值是 .
 (15)对于四面体ABCD,下列命题正确的是
(15)对于四面体ABCD,下列命题正确的是
(写出所有正确命题的编号).
①相对棱AB与CD所在的直线异面;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点;
⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
(1)i是虚数单位,若 (a、b∈R),则乘积ab的值是
(a、b∈R),则乘积ab的值是
(A)-15 (B)-3 (C)3 (D)15
(2)若集合A={x|︱2x-1︱<3},B={x|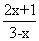 <0},则A∩B是
<0},则A∩B是
(A){x|-1<x<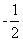 或2<x<3} (B){x|2<x<3}
或2<x<3} (B){x|2<x<3}
(C){x|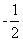 <x<2}
(D){x|-1<x<
<x<2}
(D){x|-1<x<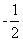 }
}
 (3)下列曲线中离心率为
(3)下列曲线中离心率为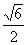 的是
的是
(A)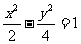 (B)
(B)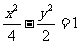
(C)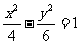 (D)
(D)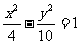

(4)下列选项中,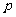 是
是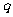 的必要不充分条件的是
的必要不充分条件的是
(A)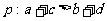 ,
, 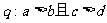
(B)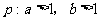 ,
, 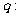
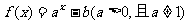 的图像不过第二象限
的图像不过第二象限
(C)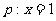 ,
,
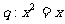
(D)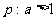 ,
,
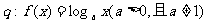 在
在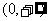 上为增函数
上为增函数
(5)已知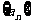 为等差数列,
为等差数列,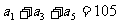 ,
,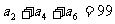 。以
。以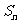 表示
表示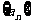 的前n项和,则使得
的前n项和,则使得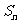 达到最大值的n是
达到最大值的n是
(A)21 (B)20 (C)19 (D)18
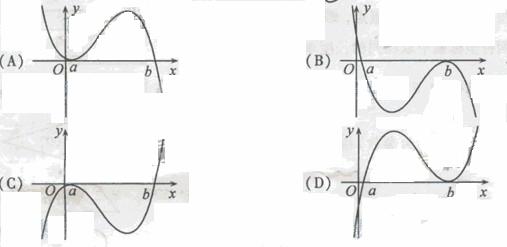
(6)设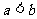 ,函数
,函数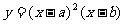 的图像可能是
的图像可能是
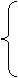
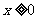
(7)若不等式组
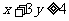 所表示的平面区域被直线
所表示的平面区域被直线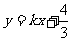 分为面积相等的两
分为面积相等的两
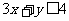
部分,则k的值是
(A)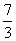 (B)
(B)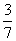 (C)
(C)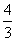 (D)
(D)
(8)已知函数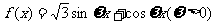 ,
,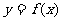 的图像与直线
的图像与直线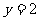 的两个相邻交点的距离等于
的两个相邻交点的距离等于 ,则
,则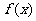 的单调递增区间是
的单调递增区间是
(A)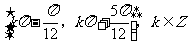 (B)
(B)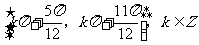
(C)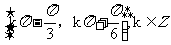 (D)
(D)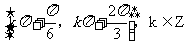
(9)已知函数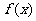 在R上满足
在R上满足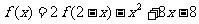 ,则曲线
,则曲线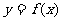 在点
在点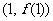 处的切线方程是
处的切线方程是
(A)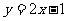
 (B)
(B)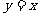 (C)
(C) (D)
(D)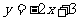
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
(A)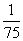 (B)
(B)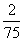 (C)
(C)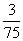 (D)
(D)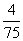
(在此卷上答题无效)
2009年普通高等学校招生全国统一考试(安徽卷)
数 学(理科)
第Ⅱ卷(非选择题 共100分)
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com