
114.证明平面与平面的垂直的思考途径
(1)转化为判断二面角是直二面角;
(2)转化为线面垂直.
113.证明直线与平面垂直的思考途径
(1)转化为该直线与平面内任一直线垂直;
(2)转化为该直线与平面内相交二直线垂直;
(3)转化为该直线与平面的一条垂线平行;
(4)转化为该直线垂直于另一个平行平面;
(5)转化为该直线与两个垂直平面的交线垂直.
112.证明直线与直线的垂直的思考途径
(1)转化为相交垂直;
(2)转化为线面垂直;
(3)转化为线与另一线的射影垂直;
(4)转化为线与形成射影的斜线垂直.
111.证明平面与平面平行的思考途径
(1)转化为判定二平面无公共点;
(2)转化为线面平行;
(3)转化为线面垂直.
110.证明直线与平面的平行的思考途径
(1)转化为直线与平面无公共点;
(2)转化为线线平行;
(3)转化为面面平行.
109.证明直线与直线的平行的思考途径
(1)转化为判定共面二直线无交点;
(2)转化为二直线同与第三条直线平行;
(3)转化为线面平行;
(4)转化为线面垂直;
(5)转化为面面平行.
91.圆的切线方程
(1)已知圆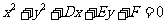 .
.
①若已知切点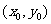 在圆上,则切线只有一条,其方程是
在圆上,则切线只有一条,其方程是
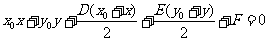 .
.
当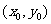 圆外时,
圆外时, 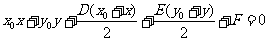 表示过两个切点的切点弦方程.
表示过两个切点的切点弦方程.
②过圆外一点的切线方程可设为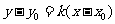 ,再利用相切条件求k,这时必有两条切线,注意不要漏掉平行于y轴的切线.
,再利用相切条件求k,这时必有两条切线,注意不要漏掉平行于y轴的切线.
③斜率为k的切线方程可设为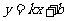 ,再利用相切条件求b,必有两条切线.
,再利用相切条件求b,必有两条切线.
(2)已知圆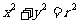 .
.
①过圆上的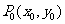 点的切线方程为
点的切线方程为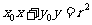 ;
;
②斜率为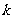 的圆的切线方程为
的圆的切线方程为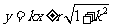 .
.
椭圆
l
椭圆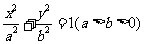 的参数方程是
的参数方程是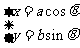 .
.
l
椭圆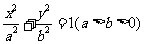 焦半径公式
焦半径公式
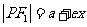 ,
,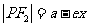 ,
,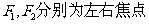
l
焦点三角形:P为椭圆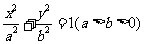 上一点,则三角形
上一点,则三角形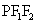 的面积S=
的面积S=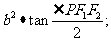 特别地,若
特别地,若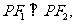 此三角形面积为
此三角形面积为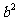 ;
;
l
在椭圆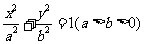 上存在点P,使
上存在点P,使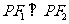 的条件是c≥b,即椭圆的离心率e的范围是
的条件是c≥b,即椭圆的离心率e的范围是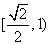 ;
;
l 椭圆的的内外部
(1)点 在椭圆
在椭圆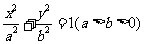 的内部
的内部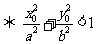 .
.
(2)点 在椭圆
在椭圆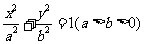 的外部
的外部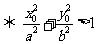 .
.
l 椭圆的切线方程
(1)椭圆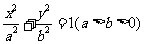 上一点
上一点 处的切线方程是
处的切线方程是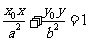 .
.
(2)过椭圆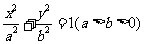 外一点
外一点 所引两条切线的切点弦方程是
所引两条切线的切点弦方程是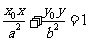 .
.
(3)椭圆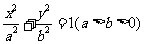 与直线
与直线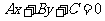 相切的条件是
相切的条件是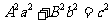 .双曲线
.双曲线
l
双曲线 的焦半径公式
的焦半径公式
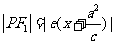 ,
,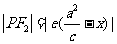 .
.
l 双曲线的内外部
(1)点 在双曲线
在双曲线 的内部
的内部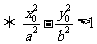 .
.
(2)点 在双曲线
在双曲线 的外部
的外部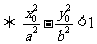 .
.
l 双曲线的方程与渐近线方程的关系
(1)若双曲线方程为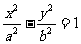
 渐近线方程:
渐近线方程: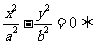
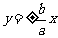 .
.
(2)若渐近线方程为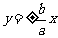
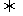
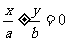
 双曲线可设为
双曲线可设为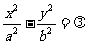 .
.
(3)若双曲线与 有公共渐近线,可设为
有公共渐近线,可设为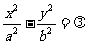 (
(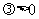 ,焦点在x轴上,
,焦点在x轴上,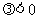 ,焦点在y轴上).
,焦点在y轴上).
l 双曲线的切线方程
(1)双曲线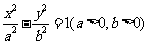 上一点
上一点 处的切线方程是
处的切线方程是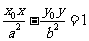 .
.
(2)过双曲线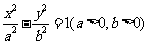 外一点
外一点 所引两条切线的切点弦方程是
所引两条切线的切点弦方程是
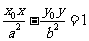 .
.
(3)双曲线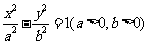 与直线
与直线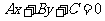 相切的条件是
相切的条件是 .
.
l 焦点到渐近线的距离等于虚半轴的长度(即b值)
抛物线
l 焦点与半径

l 焦半径公式
抛物线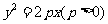 ,C
,C 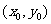 为抛物线上一点,焦半径
为抛物线上一点,焦半径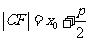 .
.
过焦点弦长 .对焦点在y轴上的抛物线有类似结论。
.对焦点在y轴上的抛物线有类似结论。
l 设点方法
抛物线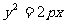 上的动点可设为P
上的动点可设为P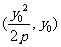 或
或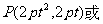 P
P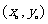 ,其中
,其中
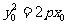 .
.
l 二次函数
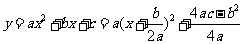
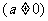 的图象是抛物线:
的图象是抛物线:
(1)顶点坐标为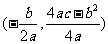 ;
;
(2)焦点的坐标为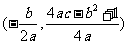 ;
;
(3)准线方程是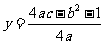 .
.
l 抛物线的内外部
(1)点 在抛物线
在抛物线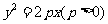 的内部
的内部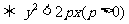 .
.
点 在抛物线
在抛物线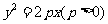 的外部
的外部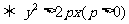 .
.
(2)点 在抛物线
在抛物线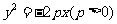 的内部
的内部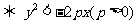 .
.
点 在抛物线
在抛物线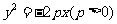 的外部
的外部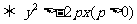 .
.
(3)点 在抛物线
在抛物线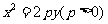 的内部
的内部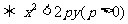 .
.
点 在抛物线
在抛物线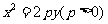 的外部
的外部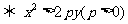 .
.
(4) 点 在抛物线
在抛物线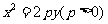 的内部
的内部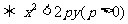 .
.
点 在抛物线
在抛物线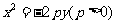 的外部
的外部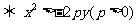 .
.
l 抛物线的切线方程
(1)抛物线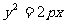 上一点
上一点 处的切线方程是
处的切线方程是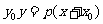 .
.
(2)过抛物线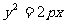 外一点
外一点 所引两条切线的切点弦方程是
所引两条切线的切点弦方程是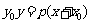 .
.
(3)抛物线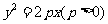 与直线
与直线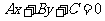 相切的条件是
相切的条件是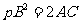 .
.
l
过抛物线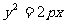 (p>0)的焦点F的直线与抛物线相交于
(p>0)的焦点F的直线与抛物线相交于

圆锥曲线共性问题
l 两个常见的曲线系方程
(1)过曲线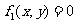 ,
,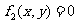 的交点的曲线系方程是
的交点的曲线系方程是
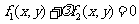 (
(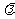 为参数).
为参数).
(2)共焦点的有心圆锥曲线系方程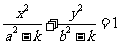 ,其中
,其中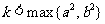 .当
.当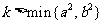 时,表示椭圆; 当
时,表示椭圆; 当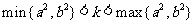 时,表示双曲线.
时,表示双曲线.
l 直线与圆锥曲线相交的弦长公式
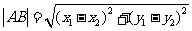 或
或
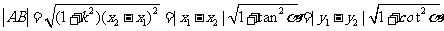
(弦端点A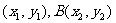
由方程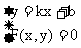 消去y得到
消去y得到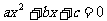 ,
, ,
,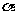 为直线
为直线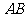 的倾斜角,
的倾斜角,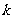 为直线的斜率).
为直线的斜率).
l
涉及到曲线上的 点A,B及线段AB的中点M的关系时,可以利用“点差法:,比如在椭圆中:
l 圆锥曲线的两类对称问题
(1)曲线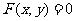 关于点
关于点 成中心对称的曲线是
成中心对称的曲线是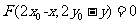 .
.
(2)曲线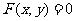 关于直线
关于直线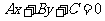 成轴对称的曲线是
成轴对称的曲线是
 .
.
l “四线”一方程
对于一般的二次曲线 ,用
,用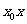 代
代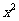 ,用
,用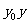 代
代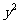 ,用
,用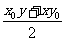 代
代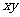 ,用
,用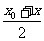 代
代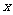 ,用
,用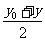 代
代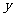 即得方程
即得方程
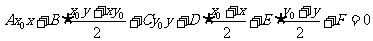 ,曲线的切线,切点弦,中点弦,弦中点方程均是此方程得到.立体几何
,曲线的切线,切点弦,中点弦,弦中点方程均是此方程得到.立体几何
85. 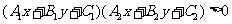 或
或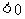 所表示的平面区域
所表示的平面区域
设曲线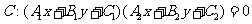 (
(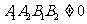 ),则
),则
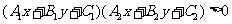 或
或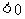 所表示的平面区域是:
所表示的平面区域是:
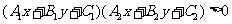 所表示的平面区域上下两部分;
所表示的平面区域上下两部分;
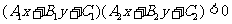 所表示的平面区域上下两部分.圆
所表示的平面区域上下两部分.圆
l 圆的四种方程
(1)圆的标准方程 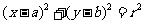 .
.
(2)圆的一般方程 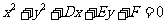 (
(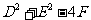 >0).
>0).
(3)圆的参数方程  .
.
(4)圆的直径式方程 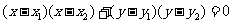 (圆的直径的端点是
(圆的直径的端点是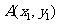 、
、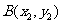 ).
).
l 圆系方程
(1)过点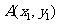 ,
,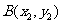 的圆系方程是
的圆系方程是
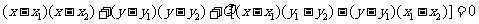
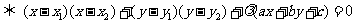 ,其中
,其中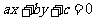 是直线
是直线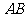 的方程,λ是待定的系数.
的方程,λ是待定的系数.
(2)过直线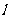 :
: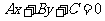 与圆
与圆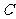 :
: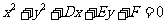 的交点的圆系方程是
的交点的圆系方程是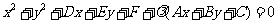 ,λ是待定的系数.
,λ是待定的系数.
(3) 过圆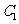 :
: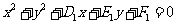 与圆
与圆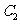 :
: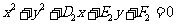 的交点的圆系方程是
的交点的圆系方程是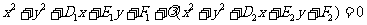 ,λ是待定的系数.
,λ是待定的系数.
l 点与圆的位置关系
点 与圆
与圆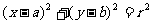 的位置关系有三种
的位置关系有三种
若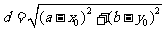 ,则
,则
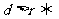 点
点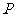 在圆外;
在圆外;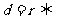 点
点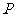 在圆上;
在圆上;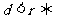 点
点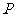 在圆内.
在圆内.
l 直线与圆的位置关系
直线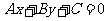 与圆
与圆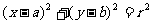 的位置关系有三种:
的位置关系有三种:
 ;
;
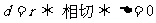 ;
;
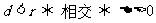 .
.
其中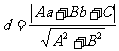 .
.
l 两圆位置关系的判定方法
设两圆圆心分别为O1,O2,半径分别为r1,r2,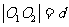
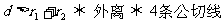 ;
;
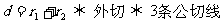 ;
;
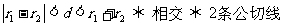 ;
;
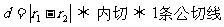 ;
;
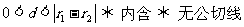 .
.
75.无理不等式
(1)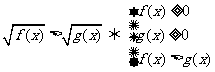 .
.
(2)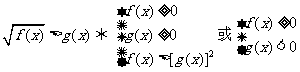 .
.
(3)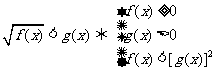 .
.
l 指数不等式与对数不等式
(1)当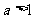 时,
时,
 ;
;
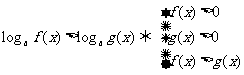 .
.
(2)当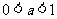 时,
时,
 ;
;
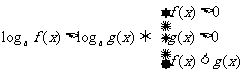
直线方程
l 斜率公式
①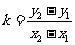 (
(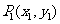 、
、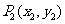 ).② k=tanα(α为直线倾斜角)
).② k=tanα(α为直线倾斜角)
l 直线的五种方程
(1)点斜式 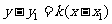 (直线
(直线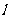 过点
过点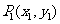 ,且斜率为
,且斜率为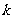 ).
).
(2)斜截式 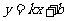 (b为直线
(b为直线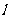 在y轴上的截距).
在y轴上的截距).
(3)两点式 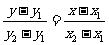 (
(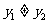 )(
)(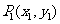 、
、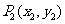 (
(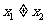 )).
)).
(4)截距式 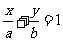 (
( 分别为直线的横、纵截距,
分别为直线的横、纵截距, )
)
(5)一般式 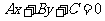 (其中A、B不同时为0).
(其中A、B不同时为0).
l 两条直线的平行和垂直
(1)若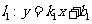 ,
,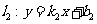
①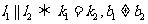 ;
;
②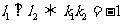 .
.
(2)若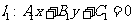 ,
,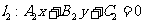 ,且A1、A2、B1、B2都不为零,
,且A1、A2、B1、B2都不为零,
①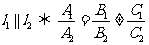 ;
;
②两直线垂直的充要条件是 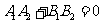 ;即:
;即: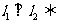
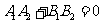
l 夹角公式
(1)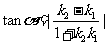 .
.
(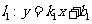 ,
,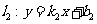 ,
,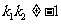 )
)
(2)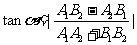 .
.
(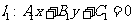 ,
,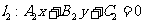 ,
,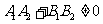 ).
).
直线 时,直线l1与l2的夹角是
时,直线l1与l2的夹角是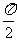 .
.
l
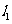 到
到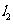 的角公式
的角公式
(1)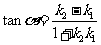 .
.
(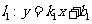 ,
,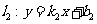 ,
,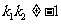 )
)
(2)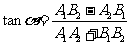 .
.
(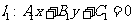 ,
,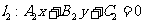 ,
,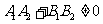 ).
).
直线 时,直线l1到l2的角是
时,直线l1到l2的角是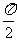 .
.
l 四种常用直线系方程
(1)定点直线系方程:经过定点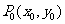 的直线系方程为
的直线系方程为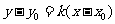 (除直线
(除直线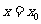 ),其中
),其中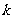 是待定的系数; 经过定点
是待定的系数; 经过定点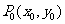 的直线系方程为
的直线系方程为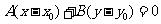 ,其中
,其中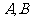 是待定的系数.
是待定的系数.
(2)共点直线系方程:经过两直线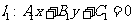 ,
,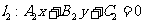 的交点的直线系方程为
的交点的直线系方程为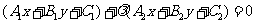 (除
(除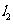 ),其中λ是待定的系数.
),其中λ是待定的系数.
(3)平行直线系方程:直线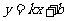 中当斜率k一定而b变动时,表示平行直线系方程.与直线
中当斜率k一定而b变动时,表示平行直线系方程.与直线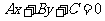 平行的直线系方程是
平行的直线系方程是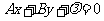 (
(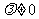 ),λ是参变量.
),λ是参变量.
(4)垂直直线系方程:与直线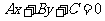 (A≠0,B≠0)垂直的直线系方程是
(A≠0,B≠0)垂直的直线系方程是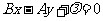 ,λ是参变量.
,λ是参变量.
l 点到直线的距离
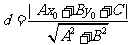 (点
(点 ,直线
,直线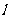 :
: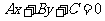 ).
).
l
 或
或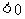 所表示的平面区域
所表示的平面区域
设直线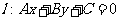 ,若A>0,则在坐标平面内从左至右的区域依次表示
,若A>0,则在坐标平面内从左至右的区域依次表示 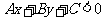 ,
, ,若A<0,则在坐标平面内从左至右的区域依次表示
,若A<0,则在坐标平面内从左至右的区域依次表示  ,
,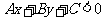 ,可记为“x 为正开口对,X为负背靠背“。(正负指X的系数A,开口对指”<>",背靠背指"><")
,可记为“x 为正开口对,X为负背靠背“。(正负指X的系数A,开口对指”<>",背靠背指"><")
39.数列的同项公式与前n项的和的关系
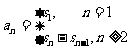 ( 数列
( 数列 的前n项的和为
的前n项的和为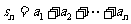 )
)
数列
l
等差数列的通项公式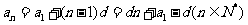 ;
;
其前n项和公式为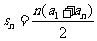
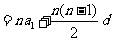
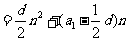 .
.
l
等比数列的通项公式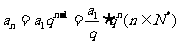 ;
;
其前n项的和公式为
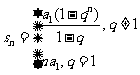 或
或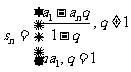 .
.
l
等比差数列 :
: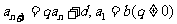 的通项公式为
的通项公式为
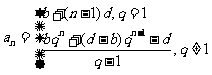 ;
;
其前n项和公式为
 .
.
l 分期付款(按揭贷款)
每次还款 元(贷款
元(贷款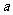 元,
元,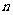 次还清,每期利率为
次还清,每期利率为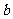 ).
).
三角函数
l 常见三角不等式
(1)若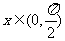 ,则
,则 .(2) 若
.(2) 若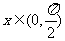 ,则
,则 .
.
(3) 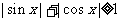 .
.
l 同角三角函数的基本关系式
 ,
,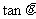 =
=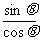 ,
, .
.
l 正弦、余弦的诱导公式

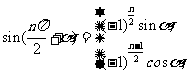

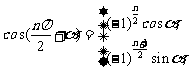
l 和角与差角公式
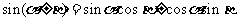 ;
;
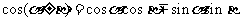 ;
;
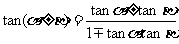 .
.
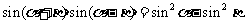 (平方正弦公式);
(平方正弦公式);
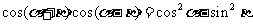 .
.
 =
=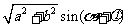 (辅助角
(辅助角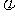 所在象限由点
所在象限由点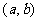 的象限决定,
的象限决定,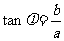 ).
).
l
半角正余切公式: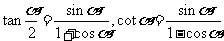
l 二倍角公式
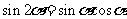 .
.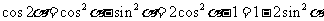 .
.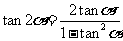 .
.
l 三倍角公式
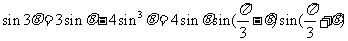 .
.
 .
.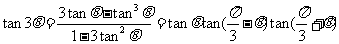 .
.
l 三角函数的周期公式
函数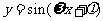 ,x∈R及函数
,x∈R及函数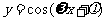 ,x∈R(A,ω,
,x∈R(A,ω,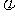 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期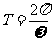 ;函数
;函数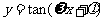 ,
,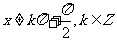 (A,ω,
(A,ω,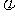 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期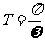 .
.
l
正弦定理 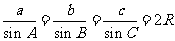 .
.
l 余弦定理
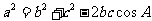 ;
;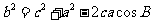 ;
;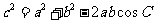 .
.
l 面积定理
(1)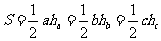 (
(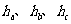 分别表示a、b、c边上的高).
分别表示a、b、c边上的高).
(2)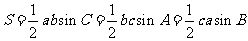 .
.
(3)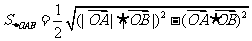 .
.
l 三角形内角和定理
在△ABC中,有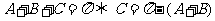
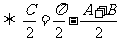
 .
.
l 在三角形中有下列恒等式:
① 
②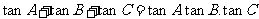
l 简单的三角方程的通解
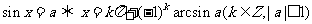 .
.
 .
.
 .
.
特别地,有
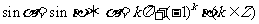 .
.
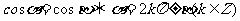 .
.
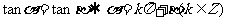 .
.
l 最简单的三角不等式及其解集
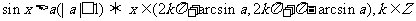 .
.
 .
.
 .
.
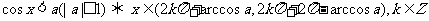 .
.
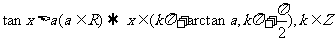 .
.
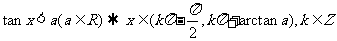 .
.
l
角的变形: 向量
向量
l 实数与向量的积的运算律
设λ、μ为实数,那么
(1) 结合律:λ(μa)=(λμ)a;
(2)第一分配律:(λ+μ)a=λa+μa;(3)第二分配律:λ(a+b)=λa+λb.
l 向量的数量积的运算律:
(1) a·b= b·a (交换律);(2)(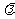 a)·b=
a)·b= 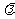 (a·b)=
(a·b)=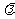 a·b= a·(
a·b= a·(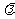 b);
b);
(3)(a+b)·c= a ·c +b·c.
l 平面向量基本定理
如果e1、e 2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数λ1、λ2,使得a=λ1e1+λ2e2.
不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底.
l 向量平行的坐标表示
设a=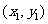 ,b=
,b=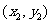 ,且b
,且b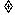 0,则a
0,则a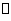 b(b
b(b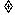 0)
0)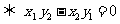 .
.
l a与b的数量积(或内积)
a·b=|a||b|cosθ.
l a·b的几何意义
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积.
l 平面向量的坐标运算
(1)设a=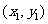 ,b=
,b=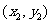 ,则a+b=
,则a+b=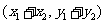 .
.
(2)设a=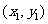 ,b=
,b=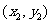 ,则a-b=
,则a-b=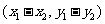 .
.
(3)设A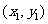 ,B
,B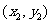 ,则
,则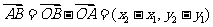 .
.
(4)设a=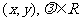 ,则
,则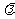 a=
a=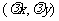 .
.
(5)设a=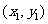 ,b=
,b=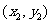 ,则a·b=
,则a·b=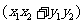 .
.
l 两向量的夹角公式
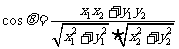 (a=
(a=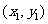 ,b=
,b=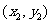 ).
).
l 平面两点间的距离公式
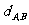 =
=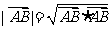
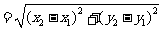 (A
(A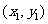 ,B
,B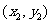 ).
).
l 向量的平行与垂直
设a=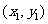 ,b=
,b=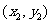 ,且b
,且b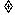 0,则
0,则
A||b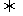 b=λa
b=λa 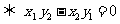 .
.
a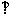 b(a
b(a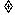 0)
0)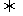 a·b=0
a·b=0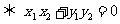 .
.
l 线段的定比分公式
设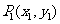 ,
,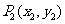 ,
,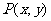 是线段
是线段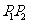 的分点,
的分点,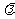 是实数,且
是实数,且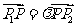 ,则
,则
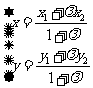
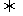
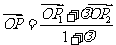
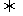
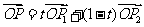 (
(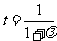 ).
).
l 三角形的重心坐标公式
△ABC三个顶点的坐标分别为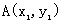 、
、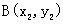 、
、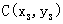 ,则△ABC的重心的坐标是
,则△ABC的重心的坐标是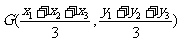 .
.
l 点的平移公式

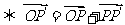 .
.
注:图形F上的任意一点P(x,y)在平移后图形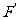 上的对应点为
上的对应点为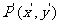 ,且
,且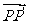 的坐标为
的坐标为 .
.
l “按向量平移”的几个结论
(1)点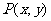 按向量a=
按向量a= 平移后得到点
平移后得到点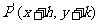 .
.
(2) 函数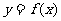 的图象
的图象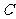 按向量a=
按向量a= 平移后得到图象
平移后得到图象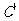 ,则
,则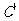 的函数解析式为
的函数解析式为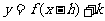 .
.
(3) 图象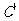 按向量a=
按向量a= 平移后得到图象
平移后得到图象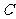 ,若
,若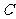 的解析式
的解析式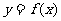 ,则
,则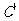 的函数解析式为
的函数解析式为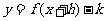 .
.
(4)曲线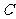 :
: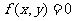 按向量a=
按向量a= 平移后得到图象
平移后得到图象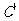 ,则
,则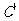 的方程为
的方程为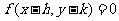 .
.
(5) 向量m=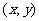 按向量a=
按向量a= 平移后得到的向量仍然为m=
平移后得到的向量仍然为m=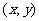 .
.
l 三角形五“心”向量形式的充要条件
设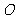 为
为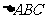 所在平面上一点,角
所在平面上一点,角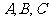 所对边长分别为
所对边长分别为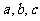 ,则
,则
(1)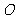 为
为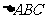 的外心
的外心 .
.
(2)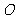 为
为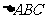 的重心
的重心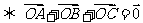 .
.
(3)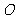 为
为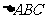 的垂心
的垂心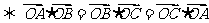 .
.
(4)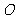 为
为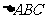 的内心
的内心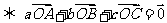 .
.
(5)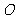 为
为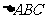 的
的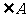 的旁心
的旁心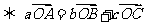 .
.
不等式
l 常用不等式:
(1)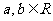

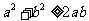 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(2)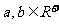

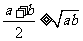 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(3)
(4)柯西不等式
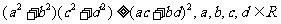
(5)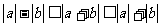 .
.
l 极值定理
已知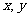 都是正数,则有
都是正数,则有
(1)若积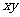 是定值
是定值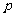 ,则当
,则当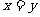 时和
时和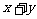 有最小值
有最小值 ;
;
(2)若和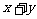 是定值
是定值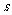 ,则当
,则当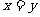 时积
时积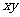 有最大值
有最大值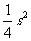 .
.
推广 已知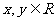 ,则有
,则有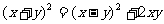
(1)若积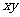 是定值,则当
是定值,则当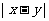 最大时,
最大时,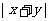 最大;
最大;
当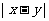 最小时,
最小时,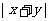 最小.
最小.
(2)若和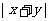 是定值,则当
是定值,则当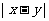 最大时,
最大时, 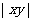 最小;
最小;
当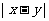 最小时,
最小时, 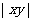 最大.
最大.
l
一元二次不等式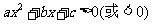
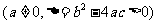 ,如果
,如果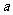 与
与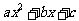 同号,则其解集在两根之外;如果
同号,则其解集在两根之外;如果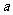 与
与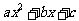 异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
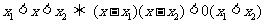 ;
;
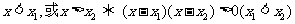 .
.
l 含有绝对值的不等式
当a> 0时,有
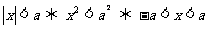 .
.
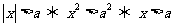 或
或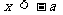 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com