
4.(2005全国Ⅲ)已知向量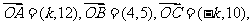 ,且A.B.C三点共线,则k= .
,且A.B.C三点共线,则k= .
3.已知向量a、b满足|a|=1,|b|=2,|a-b|=2,则|a+b|等于 ( )
A.1 B.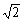 C.
C.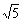 D.
D.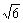
剖析:欲求|a+b|,一是设出a、b的坐标求,二是直接根据向量模计算.
2.平面上A(-2,1),B(1,4),D(4,-3),C点满足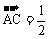
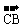 ,连DC并延长至E,使|
,连DC并延长至E,使|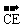 |=
|=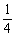 |
|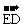 |,则点E坐标为:
( )
|,则点E坐标为:
( )
A、(-8,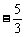 ) B、(
) B、(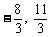 ) C、(0,1) D、(0,1)或(2,
) C、(0,1) D、(0,1)或(2,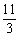 )
)
1.(2006山东)设向量a=(1,-3),b=(-2,4),c=(-1,-2),若表示向量4a、4b-2c、2(a-c)、d的有向线段依次首尾相接能构成四边形,则向量d为 ( )
A.(2,6) B.(-2,6) C.(2,-6) D.(-2,-6)
3. 设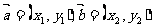 则
则
向量共线: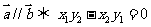
向量垂直: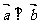 ,
,
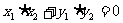
2.平面向量的坐标运算
(1)
若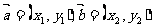 ,则
,则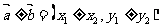
(2)
若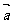 =(x,y),则
=(x,y),则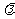
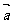 =(
=(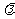 x,
x, 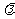 y)
y)
(3)
若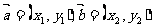 ,则
,则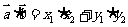
1.平面向量的坐标表示:在直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量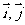 作为基底。由平面向量的基本定理知,该平面内的任一向量
作为基底。由平面向量的基本定理知,该平面内的任一向量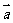 可表示成
可表示成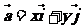 ,由于
,由于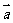 与数对(x,y)是一一对应的,因此把(x,y)叫做向量
与数对(x,y)是一一对应的,因此把(x,y)叫做向量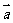 的坐标,记作
的坐标,记作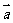 =(x,y),其中x叫作
=(x,y),其中x叫作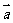 在x轴上的坐标,y叫做在y轴上的坐标。
在x轴上的坐标,y叫做在y轴上的坐标。
(1) 若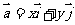 ,则
,则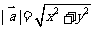
(2)若A(x1,y1),B(x2,y2)则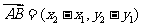 ,
,
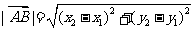
表示相等向量的有向线段的始点、终点的坐标未必相同.
(3) 向量相等ó坐标相同。
2.掌握平面向量的坐标运算,掌握共线向量的坐标表示;
1.理解平面向量的坐标概念;
26. 导数复习要注意哪些问题?
①导数的几何意义即曲线在该点处的切线的斜率,学会定义的多种变形。
②利用导数可以证明或判断函数的单调性,注意当≥0或f ’(x)≤0,带上等号。
利用导数可以证明或判断函数的单调性,注意当≥0或f ’(x)≤0,带上等号。
③f ’(x0)=0是函数f(x)在x0处取得极值的非充分非必要条件,f(x)在x0处取得极值的充分要条件是什么?
④利用导数求最值的步骤:先找定义域 再求出导数为0及导数不存在的的点,然后比较定义域的端点导数为0的点对应函数值的大小,其中最大的就是最大值,最小就为最小值。
⑤求函数极值的方法:先找定义域,再求导,找出定义域的分界点,列表求出极值。告别特别是给出函数的极大值条件,一定要验证是否在该处取得极大值 ,否则条件没有用完,这一点一定要切记。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com