
1.(2004年天津,理3)若平面向量b与向量a=(1,-2)的夹角是180°,且|b|=3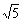 ,则b等于
( )
,则b等于
( )
A.(-3,6) B.(3,-6)
C.(6,-3) D.(-6,3)
3、运用向量的坐标表示,使向量的运算完全代数化,将数与形有机的结合。
同步练习 5.2平面向量的坐标表示
[选择题]
2、两个向量平行的坐标表示。
1、熟练运用向量的加法、减法、实数与向量的积的坐标运算法则进行运算。
[例1]平面内给定三个向量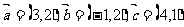 ,回答下列问题:
,回答下列问题:
(1)求满足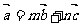 的实数m,n;
的实数m,n;
(2)若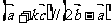 ,求实数k;
,求实数k;
(3)若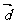 满足
满足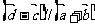 ,且
,且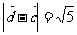 ,求
,求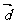
解:(1)由题意得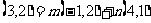
所以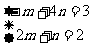 ,得
,得
(2)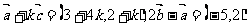
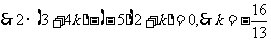
(3)设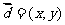 则
则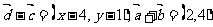
由题意得
得 或
或 ,
, 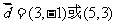
◆方法提炼:1.利用平面向量基本定理,
2.利用共线向量定理.
[例2](2006全国Ⅱ)已知向量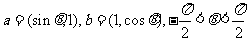 。
。
(Ⅰ)若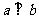 ,求
,求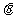 ;
;
(Ⅱ)求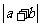 的最大值。
的最大值。
解:(Ⅰ)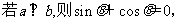
得 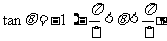 所以
所以 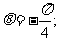
(Ⅱ) 由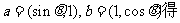
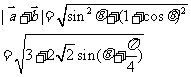
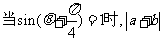 取最大值,
取最大值,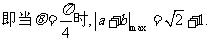
◆解题评注:向量一三角函数综合是一类常考的题目,要理解向量及运算的几何意义,要能熟练解答。
[例3]已知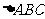 中,A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,求
中,A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,求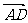 。
。
解:设D(x,y), 则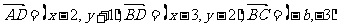
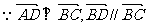
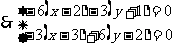 得
得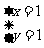
所以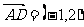
[例4]如图,设抛物线y2=2px(p>0)的焦点为F 经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴,证明直线AC经过原点O
经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴,证明直线AC经过原点O
解法一:设A(x1,y1),B(x2,y2),F( 0),则C(
0),则C(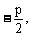 y2)
y2)
 则
则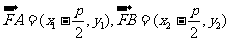
∵ 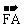 与
与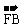 共线, ∴
共线, ∴ 
即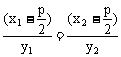 (*)
(*)
代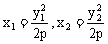 整理得,y1·y2=-p2
整理得,y1·y2=-p2
∵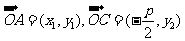
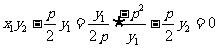
∴ 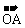 与
与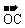 共线,即A、O、C三点共线,
共线,即A、O、C三点共线,
也就是说直线AC经过原点O
解法二:设A(x1,y1),C(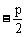 ,y2),B(x2,y2)
,y2),B(x2,y2)
欲证A、O、C共线,只需且仅需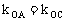 ,即
,即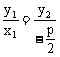 ,又
,又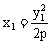
∴ 只需且仅需y1y2=-p2,用韦达定理易证明
解题评注:两向量共线的应用非常广泛,它可以处理线段(直线)平行,三点共线(多点共线)问题,使用向量的有关知识和运算方法,往往可以避免繁冗的运算,降低计算量,不仅方法新颖,而且简单明了。向量与解析几何的综合是又一命题热点。
核心步骤:
[研讨.欣赏](2005上海)在直角坐标平面中,已知点P1(1,2),P2(2,22),
P3(3,23)……Pn(n,2n),其中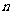 是正整数,对平面上任一点A0,记A1为A0关于点P1的对称点,A2为A1关于点P2的对称点,...,An为An-1关于点Pn的对称点。
是正整数,对平面上任一点A0,记A1为A0关于点P1的对称点,A2为A1关于点P2的对称点,...,An为An-1关于点Pn的对称点。
(1)求向量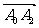 的坐标;
的坐标;
(2)当点A0在曲线C上移动时,点A2的轨迹是函数y=f(x)的图象,其中f(x)是以3为周期的周期函数,且当x∈(0,3]时,f(x)=lgx。求以曲线C为图象的函数在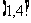 上的解析式;
上的解析式;
(3)对任意偶数n,用n表示向量 的坐标。
的坐标。
解.(1)设点A0(x,y), A0关于点P1的对称点A1的坐标为(2-x,4-y),
A1为P2关于点的对称点A2的坐标为(2+x,4+y),
∴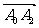 ={2,4}.
={2,4}.
(2) ∵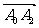 ={2,4},
={2,4},
∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到.
又x∈(3k,3k+3)时,x-3k∈(0,3), f(x)周期是3,所以f(x)=f(x-3k)=lg(x-3k)
设曲线C的函数是y=g(x),则
g(x)=f(x+2)-4=lg(x+2-3k)-4, [此时x+2∈(3k,3k+3), 即 x∈3k-2,3k+1),]
是以3为周期的周期函数.
当x∈(1,4]时,g(x)=lg(x+2-3)-4=lg(x-1)-4.
(3) =
=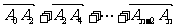 ,
,
由于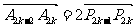 ,得
,得
 =2(
=2(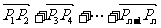 )
)
=2({1,2}+{1,23}+┄+{1,2n-1})
=2{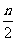 ,
, }={n,
}={n,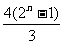 }
}
4. 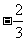 ; 5. [-6,2]; 6.(11,6). 7.
; 5. [-6,2]; 6.(11,6). 7.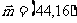 或
或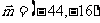
3.∵|a+b|2+|a-b|2=2(|a|2+|b|2),∴|a+b|2=2(|a|2+|b|2)-|a-b|2=6. 法2:利用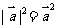
7.已知向量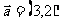 ,
,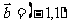 ,向量
,向量 与
与 平行,︱
平行,︱ ︱=4
︱=4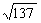 则向量
则向量 的坐标是_____________
的坐标是_____________
◆例题答案:1-3.DBD;
6.设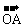 =(3,1),
=(3,1),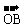 =(-1,2),
=(-1,2),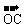 ⊥
⊥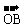 ,
,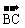 ∥
∥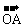 ,O为坐标原点,则满足
,O为坐标原点,则满足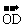 +
+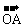 =
=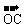 的
的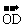 的坐标是____
的坐标是____
5.(2005湖北).已知向量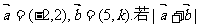 不超过5,则k的取值范围是
不超过5,则k的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com