8．(2009·保定市调研)若函数f(x)＝log₂的定义域和值域均为[1，+∞)，则实数a的取值集合为(　)

A．{0} 　　　　　　　　　　　　　　　　　　　　　　　 B．{a|0≤a≤1}

C．{a|a≥0}　 　　　　　　　　　　　　　　　　　　　 D．{a|a≥2}

答案：A

解析：由题意得，log₂≥1在x≥1时恒成立，即≥2在x≥1时恒成立；

而≥2即x++a≥2，函数g(x)＝x++a在[1，+∞)上为增函数；

∴g(x)≥g(1)＝1+1+a≥2恒成立，∴a≥0.

由g(x)在[1，+∞)上为增函数，可知f(x)在[1，+∞)也为增函数，∴f(1)＝1，∴a＝0，选A.

7．设函数f(x)＝若f(x₀)>1，则x₀的取值范围是(　)

A．(－∞，0)∪(2，+∞)　 　　　　　　　 B．(0,2)

C．(－∞，－1)∪(3，+∞)　 　　　　　 D．(－1,3)

答案：C

解析：当x₀∈[2，+∞)时，由f(x₀)＝log₂(x₀－1)>1，得x₀>3；

当x₀∈(－∞，2)时，由f(x₀)＝()x₀－1>1，得x₀<－1.所以x₀∈(－∞，－1)∪(3，+∞)．故选C.

6．已知图中曲线C₁、C₂、C₃、C₄是函数y＝log_ax的图象，则曲线C₁、C₂、C₃、C₄对应的a的值依次为(　)

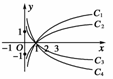
A．3、2、、　 　　　　　　　　　　　　　　　　 B．2、3、、

C．2、3、、　 　　　　　　　　　　　　　　　　 D．3、2、、

答案：B

解析：由对数函数底数与图象间的关系(在x轴上方，底数从左到右依次递增)，可知C₁、C₂、C₃、C₄对应的a的值依次为2、3、、.故选B.

5．函数y＝log(x²－5x+6)的单调增区间为(　)

A．(，+∞)　 　　　　　　　　　　　　　　　　　 B．(3，+∞)

C．(－∞，)　 　　　　　　　　　　　　　　　　　 D．(－∞，2)

答案：D

解析：由x²－5x+6>0，得x>3或x<2.当x>3时，y＝x²－5x+6为增函数；当x<2时，y＝x²－5x+6为减函数．又y＝logx为减函数，

∴所求函数的单调增区间为(－∞，2)．故选D.

4．给出下列三个等式：f(xy)＝f(x)+f(y)，f(x+y)＝f(x)f(y)，f(x+y)＝，下列函数中不满足其中任何一个等式的是(　)

A．f(x)＝3^x　 　　　　　　　　　　　　　　　　　　　 B．f(x)＝sinx

C．f(x)＝log₂x　 　　　　　　　　　　　　　　　　　 D．f(x)＝tanx

答案：B

解析：对选项A，满足f(x+y)＝f(x)f(y)；

对选项C，满足f(xy)＝f(x)+f(y)；

对选项D，满足f(x+y)＝，故选B.

3．(2009·江西协作体联考)函数f(x)＝log_a(x²+x－1)在区间[1,2]上的最大值比最小值大2，则a的值为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.或　 　　　　　　　　　　　　　　　　　　　　 D．不能确定

答案：C

解析：当0<a<1时，f(x)在[1,2]上是减函数，依题意有f(1)－f(2)＝2，即log_a1－log_a5＝2，由此解得a＝；当a>1时，f(x)在[1,2]上是增函数，依题意有f(1)－f(2)＝－2，即log_a1－log_a5＝－2，由此解得a＝.综上所述，选C.

2．(2009·石家庄市质检二)已知f(x)＝a－是定义在R上的奇函数，则f^－1(－)的值是(　)

A．－3　 　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D.

答案：A

解析：∵f(x)为奇函数，∴f(0)＝0，得a＝1，设f^－1(－)＝b，则f(b)＝－，即－＝1－，解得b＝－3.

1．(2009·石家庄市质检一)设f(x)＝log₂的反函数为f^－1(x)，若f^－1(a)＝3，则a＝(　)

A．－1　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　 D．－2

答案：A

解析：由题意，知点(3，a)在函数f(x)的图象上，所以a＝log₂＝－1.

27、某研究性学习小组欲用化学方法测量一个不规则容器的体积。把35.1g NaCl放入500 mL烧杯中，加入150 mL蒸馏水。待NaCl完全溶解后，将溶液全部转移到容器中，用蒸馏水稀释至完全充满容器。从中取出溶液100mL，该溶液恰好与20 mL 0.100 mol·L^-1AgNO₃溶液完全反应。试计算该容器的体积。

26、常温下A和B两种气体组成的混合气体(A的式量小于B的式量)，经分析混合气体中只含有氮和氢两种元素，而且，不论A和B以何种比例混合，氮和氢的质量比值总大于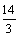。由此可确定A为　　　 ，B为　　　 ，其理由是　　　 　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　。若上述混合气体中氮和氢的质量比为7：1，则在混合气中 A 和 B 的物质的量之比为　　　　 ，A在混合气中的体积分数为　　　　　　 。