
8.(安徽卷8).若过点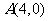 的直线
的直线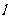 与曲线
与曲线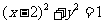 有公共点,则直线
有公共点,则直线 的斜率的取值范围为
的斜率的取值范围为
7.(天津卷2)设变量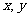 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为
的最大值为
6.(四川卷4)直线 绕原点逆时针旋转
绕原点逆时针旋转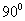 ,再向右平移1个单位,所得到的直线为
,再向右平移1个单位,所得到的直线为
5.(北京卷7)过直线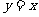 上的一点作圆
上的一点作圆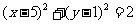 的两条切线
的两条切线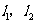 ,当直线
,当直线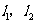 关于
关于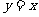 对称时,它们之间的夹角为
对称时,它们之间的夹角为
4.(北京卷5)若实数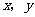 满足
满足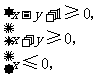 则
则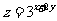 的最小值是
的最小值是
3.(全国二11)等腰三角形两腰所在直线的方程分别为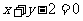 与
与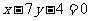 ,原点在等腰三角形的底边上,则底边所在直线的斜率为
,原点在等腰三角形的底边上,则底边所在直线的斜率为
2.(全国二5)设变量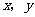 满足约束条件:
满足约束条件: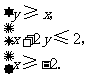 ,则
,则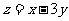 的最小值
的最小值
13.解决直线与圆的关系问题时,要充分发挥圆的平面几何性质的作用(如半径、半弦长、弦心距构成直角三角形,切线长定理、割线定理、弦切角定理等等)!
已知圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1,③圆心到直线l:x-2y=0的距离为 ,求该圆的方程.
,求该圆的方程.
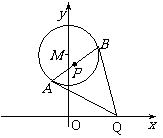 如图,已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,⑴如果
如图,已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,⑴如果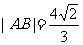 ,求直线MQ的方程;
,求直线MQ的方程;
⑵求动弦AB的中点P的轨迹方程.
课本题P75练习 2,3;P77练习2,3;P79练习2,3;P80习题 7,8,9;P84练习3,4;P87练习2,3;P87习题4,6,7;P92练习3;P96练习2,3;P96习题14,15,16,17,18 P102练习5,6;习题6,7,9,10 P106练习 3,4,5;P107练习2;P108习题5,6 7,8;
高考题1.(全国一10)若直线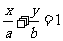 通过点
通过点 ,则( )
,则( )
A.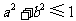 B.
B.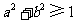 C.
C.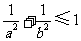 D.
D.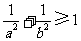
12、圆的切线与弦长:
(1)切线:
①过圆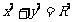 上一点
上一点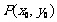 圆的切线方程是:
圆的切线方程是: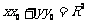 ,
,
过圆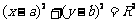 上一点
上一点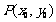 圆的切线方程是:
圆的切线方程是:
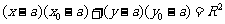 ,
,
一般地,如何求圆的切线方程?(抓住圆心到直线的距离等于半径);
②从圆外一点引圆的切线一定有两条,
设A为圆 上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为________;
上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为________;
(2)弦长问题:常用弦心距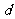 ,弦长一半
,弦长一半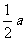 及圆的半径
及圆的半径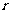 所构成的直角三角形来解:
所构成的直角三角形来解: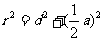 ;
;
11、圆与圆的位置关系(用两圆的圆心距与半径之间的关系判断):已知两圆的圆心分别为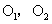 ,半径分别为
,半径分别为 ,则(1)当
,则(1)当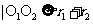 时,两圆外离;(2)当
时,两圆外离;(2)当 时,两圆外切;(3)当
时,两圆外切;(3)当 时,两圆相交;(4)当
时,两圆相交;(4)当 时,两圆内切;(5)当
时,两圆内切;(5)当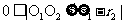 时,两圆内含。
时,两圆内含。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com