
若平面内一个动点 到一个定点
到一个定点 和一条定直线
和一条定直线 的距离之比等于一个常数
的距离之比等于一个常数 则动点的轨迹为圆锥曲线。其中定点
则动点的轨迹为圆锥曲线。其中定点 为焦点,定直线
为焦点,定直线 为准线,
为准线,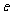 为离心率。当
为离心率。当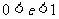 时,轨迹为椭圆;当
时,轨迹为椭圆;当 时,轨迹为抛物线;当
时,轨迹为抛物线;当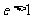 时,轨迹为双曲线。
时,轨迹为双曲线。
(1)抛物线的定义:平面内与一个定点的距离等于到一条定直线的距离点的轨迹。
其中:定点为抛物线的焦点,定直线叫做准线。
(2)抛物线的标准方程、图象及几何性质:
|
|
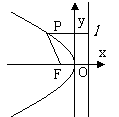
焦点在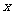 轴上, 轴上,开口向右 |
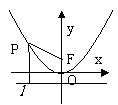
焦点在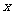 轴上, 轴上,开口向左 |
焦点在 轴上, 轴上,开口向上 |
焦点在 轴上, 轴上,开口向下 |
|
标准方程 |
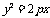 |
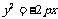 |
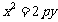 |
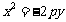 |
|
图 形 |
  |
  |
  |
  |
|
顶 点 |
 |
|||
|
对称轴 |
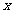 轴 轴 |
 轴 轴 |
||
|
焦 点 |
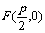 |
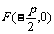 |
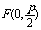 |
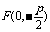 |
|
离心率 |
 |
|||
|
准 线 |
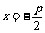 |
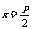 |
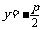 |
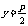 |
|
通 径 |
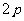 |
|||
|
焦半径 |
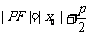 |
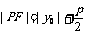 |
||
|
焦点弦 |
 (当 (当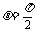 时,为 时,为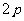 --通径) --通径) |
|||
|
焦准距 |
 |
(1)双曲线的定义:平面内与两个定点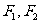 的距离的差的绝对值等于常数(小于
的距离的差的绝对值等于常数(小于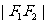 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数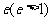 的点的轨迹。
的点的轨迹。
其中:两个定点叫做双曲线的焦点,焦点间的距离叫做焦距;定直线叫做准线。
常数叫做离心率。
注意: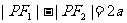 与
与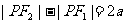 (
(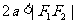 )表示双曲线的一支。
)表示双曲线的一支。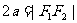 表示两条射线;
表示两条射线;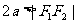 没有轨迹;
没有轨迹;
(2)双曲线的标准方程、图象及几何性质:
|
|
中心在原点,焦点在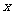 轴上 轴上 |
中心在原点,焦点在 轴上 轴上 |
||
|
标准方程 |
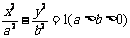 |
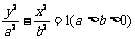 |
||
|
图 形 |
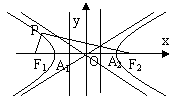 |
|
||
|
顶 点 |
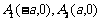 |
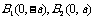 |
||
|
对称轴 |
 轴, 轴, 轴;虚轴为 轴;虚轴为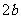 ,实轴为 ,实轴为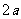 |
|||
|
焦 点 |
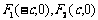 |
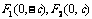 |
||
|
焦 距 |
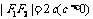 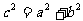 |
|||
|
离心率 |
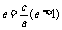 (离心率越大,开口越大) (离心率越大,开口越大) |
|||
|
准 线 |
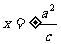 |
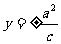 |
||
|
渐近线 |
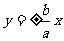 |
 |
||
|
通 径 |
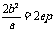 ( ( 为焦准距) 为焦准距) |
|||
|
焦半径 |
 在左支 在左支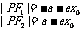 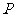 在右支 在右支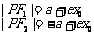 |
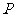 在下支 在下支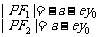 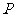 在上支 在上支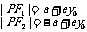 |
||
|
焦准距 |
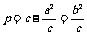 |
(3)双曲线的渐近线:
①求双曲线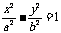 的渐近线,可令其右边的1为0,即得
的渐近线,可令其右边的1为0,即得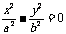 ,因式分解得到。
,因式分解得到。
②与双曲线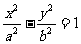 共渐近线的双曲线系方程是
共渐近线的双曲线系方程是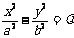 ;
;
(4)等轴双曲线为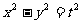 ,其离心率为
,其离心率为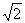
(1)椭圆的定义:平面内与两个定点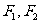 的距离的和等于常数(大于
的距离的和等于常数(大于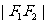 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数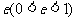 的点的轨迹。
的点的轨迹。
其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距;定直线叫做准线。
常数叫做离心率。
注意: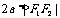 表示椭圆;
表示椭圆;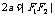 表示线段
表示线段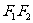 ;
;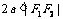 没有轨迹;
没有轨迹;
(2)椭圆的标准方程、图象及几何性质:
|
|
中心在原点,焦点在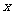 轴上 轴上 |
中心在原点,焦点在 轴上 轴上 |
||
|
标准方程 |
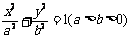 |
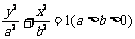 |
||
|
参数方程 |
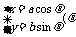 为参数) 为参数) |
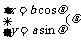 为参数) 为参数) |
||
|
图 形 |
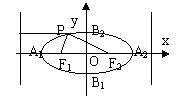 |

|
||
|
顶 点 |
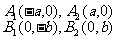 |
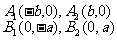 |
||
|
对称轴 |
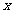 轴, 轴, 轴;短轴为 轴;短轴为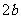 ,长轴为 ,长轴为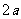 |
|||
|
焦 点 |
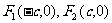 |
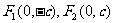 |
||
|
焦 距 |
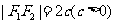 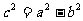 |
|||
|
离心率 |
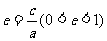 (离心率越大,椭圆越扁) (离心率越大,椭圆越扁) |
|||
|
准 线 |
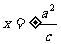 |
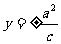 |
||
|
通 径 |
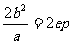 ( ( 为焦准距) 为焦准距) |
|||
|
焦半径 |
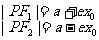 |
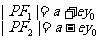 |
||
|
焦点弦 |
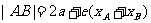 仅与它的中点的横坐标有关 |
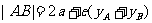 仅与它的中点的纵坐标有关 |
||
|
焦准距 |
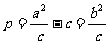 |
圆锥曲线部分
17.(浙江卷12)已知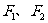 为椭圆
为椭圆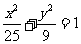 的两个焦点,过
的两个焦点,过 的直线交椭圆于A、B两点若
的直线交椭圆于A、B两点若 ,则
,则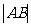 =______________。
=______________。
18已知菱形 的顶点
的顶点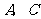 在椭圆
在椭圆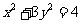 上,对角线
上,对角线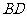 所在直线的斜率为1.
所在直线的斜率为1.
(Ⅰ)当直线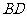 过点
过点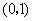 时,求直线
时,求直线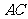 的方程;
的方程;
(Ⅱ)当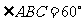 时,求菱形
时,求菱形 面积的最大值.
面积的最大值.
16.(全国一15)在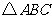 中,
中,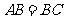 ,
,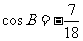 .若以
.若以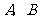 为焦点的椭圆经过点
为焦点的椭圆经过点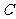 ,则该椭圆的离心率
,则该椭圆的离心率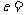 .
.
15.(全国一14)已知抛物线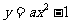 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .
14.(江西卷15)过抛物线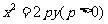 的焦点
的焦点 作倾角为
作倾角为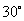 的直线,与抛物线分别交于
的直线,与抛物线分别交于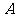 、
、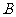 两点(
两点(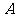 在
在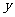 轴左侧),则
轴左侧),则 .
.
13.(江苏卷12)在平面直角坐标系中,椭圆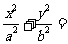 1(
1(  0)的焦距为2,以O为圆心,
0)的焦距为2,以O为圆心,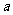 为半径的圆,过点
为半径的圆,过点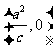 作圆的两切线互相垂直,则离心率
作圆的两切线互相垂直,则离心率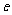 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com