
2.简答题。
(1)简述《子夜》中林佩瑶的悲剧。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(2)简述《堂吉诃德》中桑丘的总督生涯。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
[答案] (1)林佩瑶年青时与雷鸣相恋,情投意合。但不久后,雷鸣南下开始军旅生涯。林佩瑶苦等未果,只好嫁给自己不喜欢的吴荪甫。而吴荪甫独断专行,只顾事业不顾家庭,林佩瑶婚后空虚寂寞。与雷鸣的重逢加重了她的痛苦,她只能在抑郁孤独中维持不幸的婚姻。
(2)桑丘在担任总督期间,断事公平合理,为官清廉正直,制定了一系列法令,受到人们的颂扬。但终因担任总督之事是公爵夫妇的恶作剧,公爵派人伪装成敌人进攻海岛,把桑丘打得遍体鳞伤,桑丘觉得当总督的日子并不好过,于是辞官不做了。
1.下列各项中,对作品故事情节叙述不正确的两项是
( )
A.黛玉一见,便吃一大惊,心下想道:“好生奇怪,倒像在那里见过一般,何等眼熟到如此!”这是黛玉初见宝玉的心理活动。黛玉应贾政之召来到了荣国府。宝黛初见,两人竟然都有似曾相识的感觉,为此后两个人之间的感情奠定了基础。(《红楼梦》)
B.聂赫留朵夫坐上马,车离开库兹明斯科耶,前往他从姑妈名下继承下来的那个田庄--就是他和卡秋莎相识的那个地方。对于这个田庄上的土地,他也想用库兹明斯科耶的那种办法加以处理。此外,他还打听了当年他抛弃卡秋莎后她和她孩子的情况。
C.冯乐山在生日宴席上向高家提起了亲事--要把自己的侄孙女许配给觉民,高老太爷一口应允。正在与钱梅芬处于热恋中的觉民当即表示反对。觉新把觉民的意见向祖父解释了一下,祖父立刻生气地驳斥道:“我说是对的,那个敢说不对?我说怎样做,就要怎样做!”(《家》)
D.帐上袁术大喝曰:“汝欺吾众诸侯无大将耶?量一弓手,安敢乱言!与我打出!”曹操急止之曰:“公路息怒。此人既出大言,必有勇略;试教出马,如其不胜,责之未迟。”
各路诸侯共讨董卓。董卓派华雄迎战。华雄连斩两员盟军猛将。关羽毛遂自荐,愿取华雄性命。袁术、曹操对此反应不一,从这里可以看出他二人的性格特点。(《三国演义》)
E.葛朗台推门进来,一眼就盯住了那闪亮的东西。老头儿身子一纵,扑上梳妆匣,好似一头老虎扑上一个睡着的婴儿。他瞅着女儿,仿佛她是金铸的一般。
欧也妮同情堂弟的破产,把自己全部积蓄六千法郎送给他作去印度的盘缠,查理回赠给他一个母亲留给他的镶金首饰盒。守财奴葛朗台看到金子就发狂。(《欧也妮·葛朗台》)
[解析] A项应是贾母让黛玉到荣国府的;C项觉民应是与琴热恋。
[答案] AC
1 函数y=cos2(x-
函数y=cos2(x-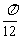 )+sin2(x+
)+sin2(x+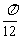 )-1是( )
)-1是( )
A 奇函数而不是偶函数
B
奇函数而不是偶函数
B 偶函数而不是奇函数
偶函数而不是奇函数
C 奇函数且是偶函数
D
奇函数且是偶函数
D 非奇非偶函数
非奇非偶函数
2 函数y=sin(2x+
函数y=sin(2x+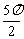 )图象的一条对称轴方程是( )
)图象的一条对称轴方程是( )
A x=-
x=-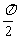 B
B x=-
x=- C
C x=
x=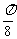 D
D x=
x=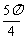
3 设条件甲为“y=Asin(ωx+φ)是偶函数”,条件乙为“φ=
设条件甲为“y=Asin(ωx+φ)是偶函数”,条件乙为“φ=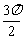 ”,则甲是乙的( )
”,则甲是乙的( )
A 充分非必要条件
B
充分非必要条件
B 必要非充分条件
必要非充分条件
C 充要条件
D
充要条件
D 既不充分也不必要条件
既不充分也不必要条件
4 函数y=sin4x+cos4x的最小正周期为
.
函数y=sin4x+cos4x的最小正周期为
.
5 函数y=sin2xtanx的值域为
函数y=sin2xtanx的值域为

6 函数y=x-sinx,x∈[0,π]的最大值为( )
函数y=x-sinx,x∈[0,π]的最大值为( )
A 0
B
0
B
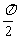 -1
C
-1
C π D
π D
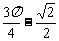
7 求函数y=2sin22x+4sin2xcos2x+3cos22x的最小正周期
求函数y=2sin22x+4sin2xcos2x+3cos22x的最小正周期
8 求函数f(x)=sin6x+cos6x的最小正周期,并求f(x)的最大值和最小值
求函数f(x)=sin6x+cos6x的最小正周期,并求f(x)的最大值和最小值
9 已知f(x)=
已知f(x)= ,问x在[0,π]上取什么值时,f(x)取到最大值和最小值
,问x在[0,π]上取什么值时,f(x)取到最大值和最小值
例1 求下列函数的周期:
(1)y=3cosx,x∈R;
(2)y=sin2x,x∈R;
(3)y=2sin( x-
x-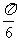 ),x∈R
),x∈R
解:(1)∵y=cosx的周期是2π
∴只有x增到x+2π时,函数值才重复出现
∴y=3cosx,x∈R的周期是2π
(2)令Z=2x,那么x∈R必须并且只需Z∈R,且函数y=sinZ,Z∈R的周期是2π
即Z+2π=2x+2π=2(x+π).
只有当x至少增加到x+π,函数值才能重复出现
∴y=sin2x的周期是π
(3)令Z= x-
x-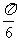 ,那么x∈R必须并且只需Z∈R,且函数y=2sinZ,Z∈R的周期是2π,由于Z+2π=(
,那么x∈R必须并且只需Z∈R,且函数y=2sinZ,Z∈R的周期是2π,由于Z+2π=( x-
x-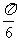 )+2π=
)+2π= (x+4π)-
(x+4π)-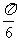 ,所以只有自变量x至少要增加到x+4π,函数值才能重复取得,即T=4π是能使等式2sin[
,所以只有自变量x至少要增加到x+4π,函数值才能重复取得,即T=4π是能使等式2sin[ (x+T)-
(x+T)-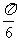 ]=2sin(
]=2sin( x-
x-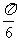 )成立的最小正数
)成立的最小正数
从而y=2sin( x-
x-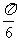 ),x∈R的周期是4π
),x∈R的周期是4π
从上述可看出,这些函数的周期仅与自变量x的系数有关
一般地,函数y=Asin(ωx+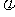 ),x∈R及函数y=Acos(ωx+
),x∈R及函数y=Acos(ωx+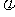 ),x∈R(其中A、ω、
),x∈R(其中A、ω、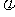 为常数,且A≠0,ω>0)的周期T=
为常数,且A≠0,ω>0)的周期T=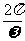

根据这个结论,我们可以由这类函数的解析式直接写出函数的周期,如对于上述例子:
(1)T=2π,(2)T=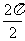 =π,(3)T=2π÷
=π,(3)T=2π÷ =4π
=4π
例2不通过求值,指出下列各式大于0还是小于0
(1)sin(-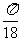 )-sin(-
)-sin(- );
);
(2)cos(-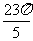 )-cos(-
)-cos(-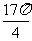 ).
).
解:(1)∵- <-
<- <-
<-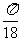 <
< .
.
且函数y=sinx,x∈[- ,
, ]是增函数
]是增函数
∴sin(- )<sin(-
)<sin(-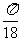 )
)
即sin(-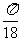 )-sin(-
)-sin(- )>0
)>0
(2)cos(-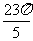 )=cos
)=cos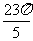 =cos
=cos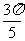
cos(-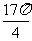 )=cos
)=cos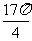 =cos
=cos
∵0< <
<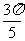 <π
<π
且函数y=cosx,x∈[0,π]是减函数
∴cos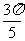 <cos
<cos
即cos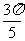 -cos
-cos <0
<0
∴cos(-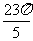 )-cos(-
)-cos(-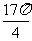 )<0
)<0
例3 求函数y=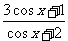 的值域
的值域
解:由已知:cosx=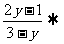 |
| |=|cosx|≤1
|=|cosx|≤1 (
( )2≤1
)2≤1 3y2+2y-8≤0
3y2+2y-8≤0
∴-2≤y≤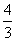
∴ymax=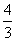 ,ymin=-2
,ymin=-2
例4 f(x)=sinx图象的对称轴是
f(x)=sinx图象的对称轴是

解:由图象可知:
对称轴方程是:x=kπ+ (k∈Z)
(k∈Z)
例5 (1)函数y=sin(x+
(1)函数y=sin(x+ )在什么区间上是增函数?
)在什么区间上是增函数?
(2)函数y=3sin(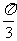 -2x)在什么区间是减函数?
-2x)在什么区间是减函数?
解:(1)函数y=sinx在下列区间上是增函数:
2kπ- <x<2kπ+
<x<2kπ+ (k∈Z)
(k∈Z)
∴函数y=sin(x+ )为增函数,当且仅当2kπ-
)为增函数,当且仅当2kπ- <x+
<x+ <2kπ+
<2kπ+ 即2kπ-
即2kπ-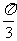 <x<2kπ+
<x<2kπ+ (k∈Z)为所求
(k∈Z)为所求
(2)∵y=3sin(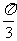 -2x)=-3sin(2x-
-2x)=-3sin(2x-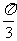 )
)
由2kπ- ≤2x-
≤2x-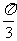 ≤2kπ+
≤2kπ+
得kπ- ≤x≤kπ+
≤x≤kπ+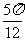 (k∈Z)为所求
(k∈Z)为所求
或:令u=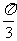 -2x,则u是x的减函数
-2x,则u是x的减函数
又∵y=sinu在[2kπ- ,2kπ+
,2kπ+ ](k∈Z)上为增函数,
](k∈Z)上为增函数,
∴原函数y=3sin(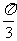 -2x)在区间[2kπ-
-2x)在区间[2kπ- ,2kπ+
,2kπ+ ]上递减
]上递减
设2kπ- ≤
≤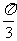 -2x≤2kπ+
-2x≤2kπ+
解得kπ- ≤x≤kπ+
≤x≤kπ+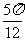 (k∈Z)
(k∈Z)
∴原函数y=3sin(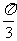 -2x)在[kπ-
-2x)在[kπ- ,kπ+
,kπ+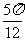 ](k∈Z)上单调递减
](k∈Z)上单调递减
7.单调性
正弦函数在每一个闭区间[- +2kπ,
+2kπ, +2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[
+2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[ +2kπ,
+2kπ, +2kπ](k∈Z)上都是减函数,其值从1减小到-1
+2kπ](k∈Z)上都是减函数,其值从1减小到-1
余弦函数在每一个闭区间[(2k-1)π,2kπ](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2kπ,(2k+1)π](k∈Z)上都是减函数,其值从1减小到-1
6.奇偶性
y=sinx为奇函数,y=cosx为偶函数
正弦曲线关于原点O对称,余弦曲线关于y轴对称
5.周期性
一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期
1°周期函数xÎ定义域M,则必有x+TÎM, 且若T>0则定义域无上界;T<0则定义域无下界;
2°“每一个值”只要有一个反例,则f (x)就不为周期函数(如f (x0+t)¹f (x0))
3°T往往是多值的(如y=sinx 2p,4p,…,-2p,-4p,…都是周期)周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期)
正弦函数、余弦函数都是周期函数,2kπ(k∈Z且k≠0)都是它的周期,最小正周期是2π
4.值域
正弦函数、余弦函数的值域都是[-1,1]
其中正弦函数y=sinx,x∈R
①当且仅当x= +2kπ,k∈Z时,取得最大值1
+2kπ,k∈Z时,取得最大值1
②当且仅当x=- +2kπ,k∈Z时,取得最小值-1
+2kπ,k∈Z时,取得最小值-1
而余弦函数y=cosx,x∈R
①当且仅当x=2kπ,k∈Z时,取得最大值1
②当且仅当x=(2k+1)π,k∈Z时,取得最小值-1
3.定义域:
正弦函数、余弦函数的定义域都是实数集R[或(-∞,+∞)],
分别记作: y=sinx,x∈R y=cosx,x∈R
2.用五点法作正弦函数和余弦函数的简图(描点法):
正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:
(0,0) (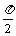 ,1) (p,0) (
,1) (p,0) (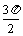 ,-1) (2p,0)
,-1) (2p,0)
余弦函数 y=cosx xÎ[0,2p]的五个点关键是
y=cosx xÎ[0,2p]的五个点关键是
(0,1) (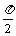 ,0) (p,-1) (
,0) (p,-1) (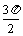 ,0) (2p,1)
,0) (2p,1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com