
3.已知命题p、q,“非p为真命题”是“p或q是假命题”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
2.与函数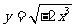 有相同图象的一个函数是 ( )
有相同图象的一个函数是 ( )
A.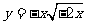 B.
B.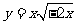
C.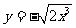 D.
D.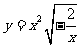
1.若集合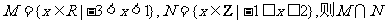 = ( )
= ( )
A.{0} B.{-1,0} C.{-1,0,1} D.{-2,-1,0,1,2}
指数形式的函数定义域、值域的求法,判断其单调性和奇偶性的方法
求下列函数的定义域和值域:
⑴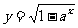 ⑵
⑵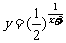
解:⑴要使函数有意义,必须
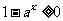 ,
, 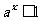
当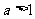 时
时 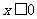 ; 当
; 当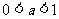 时
时 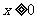
∵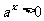 ∴
∴ ∴值域为
∴值域为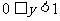
⑵要使函数有意义,必须 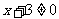 即
即 
∵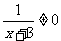 ∴
∴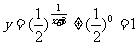
又∵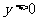 ∴值域为
∴值域为 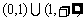
例1求下列函数的定义域、值域:
⑴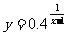 ⑵
⑵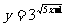 ⑶
⑶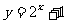

分析:此题要利用指数函数的定义域、值域,并结合指数函数的图象 注意向学生指出函数的定义域就是使函数表达式有意义的自变量x的取值范围
注意向学生指出函数的定义域就是使函数表达式有意义的自变量x的取值范围
解(1)由x-1≠0得x≠1
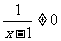 所以,所求函数定义域为{x|x≠1}
所以,所求函数定义域为{x|x≠1}
由
,得y≠1
所以,所求函数值域为{y|y>0且y≠1}
说明:对于值域的求解,在向学生解释时,可以令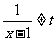 ,考察指数函数y=
,考察指数函数y=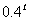 ,并结合图象直观地得到,以下两题可作类似处理
,并结合图象直观地得到,以下两题可作类似处理
(2)由5x-1≥0得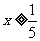

所以,所求函数定义域为{x|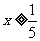 }
}
由 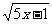 ≥0得y≥1
≥0得y≥1
所以,所求函数值域为{y|y≥1}
(3)所求函数定义域为R
由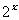 >0可得
>0可得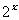 +1>1
+1>1
所以,所求函数值域为{y|y>1}
通过此例题的训练,学会利用指数函数的定义域、值域去求解指数形式的复合函数的定义域、值域,还应注意书写步骤与格式的规范性
例2求函数 的单调区间,并证明
的单调区间,并证明
解:设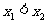
则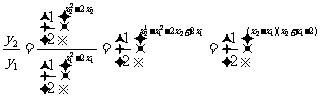
∵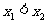 ∴
∴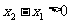
当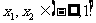 时,
时,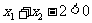 这时
这时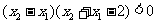
即 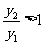 ∴
∴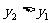 ,函数单调递增
,函数单调递增
当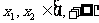 时,
时, 这时
这时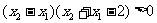
即 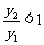 ∴
∴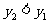 ,函数单调递减
,函数单调递减
∴函数y在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
解法二、(用复合函数的单调性):
设: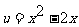 则:
则:
对任意的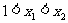 ,有
,有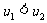 ,又∵
,又∵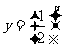 是减函数
是减函数
∴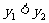 ∴
∴ 在
在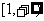 是减函数
是减函数
对任意的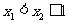 ,有
,有 ,又∵
,又∵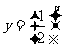 是减函数
是减函数
∴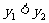 ∴
∴ 在
在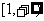 是增函数
是增函数
引申:求函数 的值域 (
的值域 (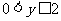 )
)
小结:复合函数单调性的判断(见第8课时)
例3设a是实数,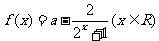
试证明对于任意a,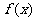 为增函数;
为增函数;
分析:此题虽形式较为复杂,但应严格按照单调性、奇偶性的定义进行证明 还应要求学生注意不同题型的解答方法
还应要求学生注意不同题型的解答方法
(1)证明:设 ∈R,且
∈R,且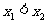
则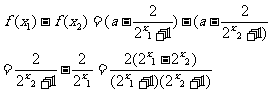

由于指数函数
y=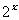 在R上是增函数,且
在R上是增函数,且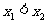 ,
,
所以
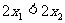 即
即
 <0,
<0,
又由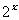 >0得
>0得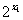 +1>0,
+1>0,  +1>0
+1>0
所以 <0即
<0即
因为此结论与a取值无关,所以对于a取任意实数,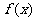 为增函数
为增函数
评述:上述证明过程中,在对差式正负判断时,利用了指数函数的值域及单调性
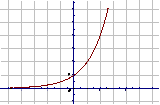
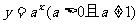 的图象和性质
的图象和性质
|
|
a>1 |
0<a<1 |
|
图 象 |
 |
 |
|
性 质 |
(1)定义域:R |
|
|
(2)值域:(0,+∞) |
||
|
(3)过点(0,1),即x=0时,y=1 |
||
|
(4)在 R上是增函数 |
(4)在R上是减函数 |
22.(本小题满分14分)
已知函数f(x)的定义域为(0,+∞),且对任意的正实数x,y都有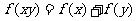 ,且当x>1时,f(x)>0,f(4)=1.
,且当x>1时,f(x)>0,f(4)=1.
(1) 求证:f(1)=0;
(2)
求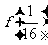 ;
;
(3) 求证:f(x)在(0,+∞)上为增函数;
(4)
解不等式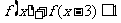 .
.
21.(本小题满分12分)
已知二次函数g(x)的图象经过坐标原点,且满足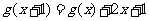 。设函数
。设函数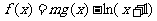 ,其中m为非零常数.
,其中m为非零常数.
(1)求函数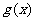 的解析式;
的解析式;
(2)当-2<m<0时,判断函数f(x)的单调性并且说明理由;
(3)证明:对任意的正整数n,不等式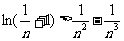 恒成立.
恒成立.
20.(本小题满分12分)
已知函数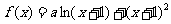 在x=1处有极值.
在x=1处有极值.
(1) 求实数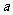 的值;
的值;
(2) 求函数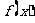 的单调区间;
的单调区间;
(3) 令g(x)=  ,若曲线g(x)在(1,g(1))处的切线与两坐标轴分别交于A、B两点(
,若曲线g(x)在(1,g(1))处的切线与两坐标轴分别交于A、B两点(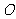 为坐标原点),求
为坐标原点),求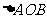 的面积.
的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com