
10、直线与圆的位置关系:直线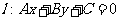 和圆
和圆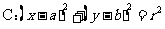
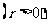 有相交、相离、相切。可从代数和几何两个方面来判断:
有相交、相离、相切。可从代数和几何两个方面来判断:
(1)代数方法(判断直线与圆方程联立所得方程组的解的情况):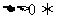 相交;
相交;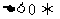 相离;
相离;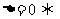 相切;
相切;
(2)几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为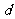 ,则
,则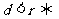 相交;
相交;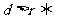 相离;
相离;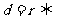 相切。
相切。
提醒:判断直线与圆的位置关系一般用几何方法较简捷。
如(1)圆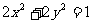 与直线
与直线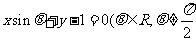
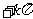 ,
,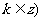 的位置关系为____;
的位置关系为____;
(2)若直线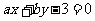 与圆
与圆 切于点
切于点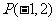 ,则
,则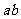 的值____;
的值____;
(3)直线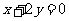 被曲线
被曲线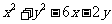
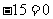 所截得的弦长等于 ;
所截得的弦长等于 ;
(4)一束光线从点A(-1,1)出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 ;
(5)已知圆C: ,直线L:
,直线L: 。①求证:对
。①求证:对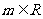 ,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若
,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若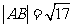 ,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程.
,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程.
9、点与圆的位置关系:已知点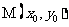 及圆
及圆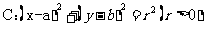 ,(1)点M在圆C外
,(1)点M在圆C外 ;(2)点M在圆C内
;(2)点M在圆C内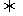
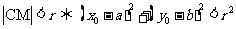 ;(3)点M在圆C上
;(3)点M在圆C上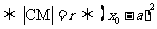
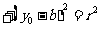 。
。
如点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是______
8、圆的方程:
⑴圆的标准方程: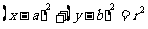 。
。
⑵圆的一般方程: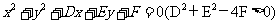 ,
,
特别提醒:只有当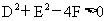 时,方程
时,方程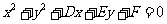 才表示圆心为
才表示圆心为 ,半径为
,半径为 的圆
的圆
(二元二次方程 表示圆的充要条件是什么? (
表示圆的充要条件是什么? (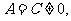 且
且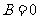 且
且 ));
));
(3)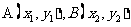 为直径端点的圆方程
为直径端点的圆方程
如(1)圆C与圆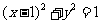 关于直线
关于直线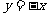 对称,则圆C的方程为____________;
对称,则圆C的方程为____________;
(2)圆心在直线 上,且与两坐标轴均相切的圆的标准方程是__________;
上,且与两坐标轴均相切的圆的标准方程是__________;
(3)如果直线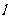 将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么
将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么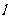 的斜率的取值范围是;
的斜率的取值范围是;
(4)方程x2+y2-x+y+k=0表示一个圆,则实数k的取值范围为____;
7、对称(中心对称和轴对称)问题--代入法:
如(1)已知点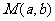 与点
与点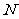 关于
关于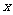 轴对称,点P与点N关于
轴对称,点P与点N关于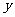 轴对称,点Q与点P关于直线
轴对称,点Q与点P关于直线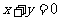 对称,则点Q的坐标为_______;
对称,则点Q的坐标为_______;
(2)已知直线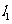 与
与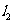 的夹角平分线为
的夹角平分线为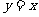 ,若
,若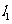 的方程为
的方程为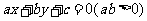 ,那么
,那么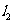 的方程是___________;
的方程是___________;
(3)点A(4,5)关于直线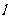 的对称点为B(-2,7),则
的对称点为B(-2,7),则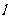 的方程是_________;
的方程是_________;
(4)已知一束光线通过点A(-3,5),经直线 :3x-4y+4=0反射。如果反射光线通过点B(2,15),则反射光线所在直线的方程是_________;
:3x-4y+4=0反射。如果反射光线通过点B(2,15),则反射光线所在直线的方程是_________;
(5)已知ΔABC顶点A(3,-1),AB边上的中线所在直线的方程为6x+10y-59=0,∠B的平分线所在的方程为x-4y+10=0,求BC边所在的直线方程;
提醒:在解几中遇到角平分线、光线反射等条件常利用对称求解。
6、直线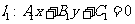 与直线
与直线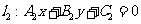 的位置关系:
的位置关系:
(1)平行
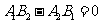 (斜率)且
(斜率)且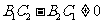 (在
(在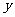 轴上截距);
轴上截距);
(2)相交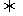
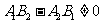 ;
;
(3)重合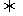
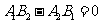 且
且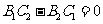 。
。
提醒:(1) 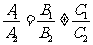 、
、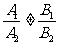 、
、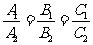 仅是两直线平行、相交、重合的充分不必要条件!为什么?
仅是两直线平行、相交、重合的充分不必要条件!为什么?
(2)在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中提到的两条直线都是指不重合的两条直线;
(3)直线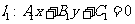 与直线
与直线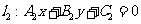 垂直
垂直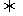
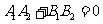 。如(1)设直线
。如(1)设直线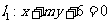 和
和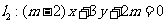 ,当
,当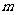 =_______时
=_______时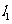 ∥
∥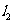 ;
;
当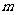 =________时
=________时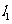
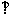
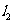 ;当
;当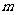 _________时
_________时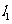 与
与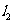 相交;当
相交;当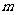 =_________时
=_________时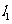 与
与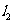 重合;
重合;
(2)已知直线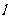 的方程为
的方程为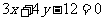 ,则与
,则与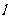 平行,且过点(-1,3)的直线方程是______;
平行,且过点(-1,3)的直线方程是______;
(3)两条直线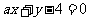 与
与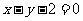 相交于第一象限,则实数
相交于第一象限,则实数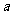 的取值范围是__;
的取值范围是__;
(4)设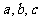 分别是△ABC中∠A、∠B、∠C所对边的边长,则直线
分别是△ABC中∠A、∠B、∠C所对边的边长,则直线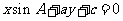 与
与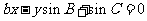 的位置关系是____;
的位置关系是____;
5、点到直线的距离及两平行直线间的距离:
(1)点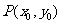 到直线
到直线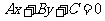 的距离
的距离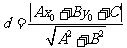 ;
;
(2)两平行线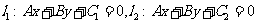 间的距离为
间的距离为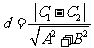 。
。
4.设直线方程的一些常用技巧:
(1)知直线纵截距 ,常设其方程为
,常设其方程为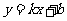 ;
;
(2)知直线横截距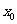 ,常设其方程为
,常设其方程为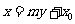 (它不适用于斜率为0的直线);
(它不适用于斜率为0的直线);
(3)知直线过点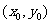 ,当斜率
,当斜率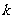 存在时,常设其方程为
存在时,常设其方程为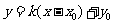 ,当斜率
,当斜率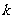 不存在时,则其方程为
不存在时,则其方程为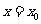 ;
;
(4)与直线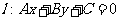 平行的直线可表示为
平行的直线可表示为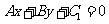 ;
;
(5)与直线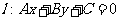 垂直的直线可表示为
垂直的直线可表示为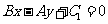 .
.
提醒:求直线方程的基本思想和方法是恰当选择方程的形式,利用待定系数法求解。
3、直线的方程:
(1)点斜式:已知直线过点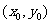 斜率为
斜率为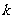 ,则直线方程为
,则直线方程为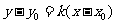 ,它不包括垂直于
,它不包括垂直于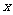 轴的直线。
轴的直线。
(2)斜截式:已知直线在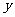 轴上的截距为
轴上的截距为 和斜率
和斜率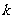 ,则直线方程为
,则直线方程为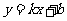 ,它不包括垂直于
,它不包括垂直于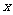 轴的直线。
轴的直线。
(3)两点式:已知直线经过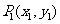 、
、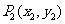 两点,则直线方程为
两点,则直线方程为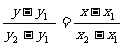 ,它不包括垂直于坐标轴的直线。
,它不包括垂直于坐标轴的直线。
(4)截距式:已知直线在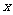 轴和
轴和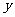 轴上的截距为
轴上的截距为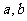 ,则直线方程为
,则直线方程为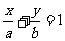 ,它不包括垂直于坐标轴的直线和过原点的直线。
,它不包括垂直于坐标轴的直线和过原点的直线。
(5)一般式:任何直线均可写成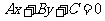 (A,B不同时为0)的形式。
(A,B不同时为0)的形式。
如(1)经过点(2,1)且方向向量为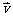 =(-1,
=(-1,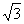 )的直线的点斜式方程是___________;
)的直线的点斜式方程是___________;
(2)直线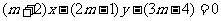 ,不管
,不管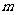 怎样变化恒过点______;
怎样变化恒过点______;
(3)若曲线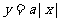 与
与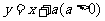 有两个公共点,则
有两个公共点,则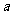 的取值范围是_______
的取值范围是_______
(4)过点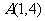 ,且纵横截距的绝对值相等的直线共有___条
,且纵横截距的绝对值相等的直线共有___条
2、直线的斜率:
(1)定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率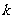 ,即
,即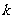 =tan
=tan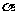 (
(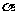 ≠90°);倾斜角为90°的直线没有斜率;
≠90°);倾斜角为90°的直线没有斜率;
(2)斜率公式:经过两点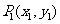 、
、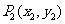 的直线的斜率为
的直线的斜率为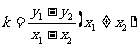 ;(3)直线的方向向量
;(3)直线的方向向量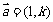 ,直线的方向向量与直线的斜率有何关系?
,直线的方向向量与直线的斜率有何关系?
(4)应用:证明三点共线: 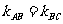 。
。
如(1) 两条直线钭率相等是这两条直线平行的____________条件;
(2)实数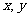 满足
满足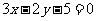 (
(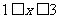 ),则
),则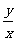 的最大值、最小值分别为______
的最大值、最小值分别为______
1、直线的倾斜角:
(1)定义:在平面直角坐标系中,对于一条与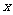 轴相交的直线
轴相交的直线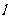 ,如果把
,如果把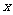 轴绕着交点按逆时针方向转到和直线
轴绕着交点按逆时针方向转到和直线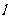 重合时所转的最小正角记为
重合时所转的最小正角记为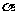 ,那么
,那么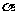 就叫做直线的倾斜角。当直线
就叫做直线的倾斜角。当直线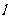 与
与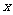 轴重合或平行时,规定倾斜角为0;
轴重合或平行时,规定倾斜角为0;
(2)倾斜角的范围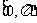 。
。
如(1)直线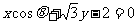 的倾斜角的范围是__
__;
的倾斜角的范围是__
__;
(2)过点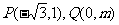 的直线的倾斜角的范围
的直线的倾斜角的范围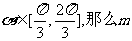 值的范围是__
值的范围是__
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com