
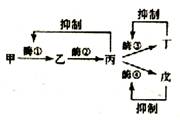
2.右图是某种微生物体内某一物质代谢过程的示意图。
下列有关酶活性调节的叙述,错误的是
A.丁物质既是酶③催化生成的产物,又是酶③的反馈抑制物
B.戊物质通过与酶④结成导致酶④结构变化而使其活性下降
C.当丁物质和戊物质中任意一种过量时,酶①的活性都将受到抑制
D.若此代谢途径的终产物不断排出菌体外,可消除丙物质对酶①的抑制作用
1.下列关于人类遗传病的叙述,错误的是
A.单基因突变可以导致遗传病
B.染色体结构的改变可以导致遗传病
 C.近亲婚配可增加隐性遗传病的发病风险
C.近亲婚配可增加隐性遗传病的发病风险
D.环境因素对多基因遗传病的发病无影响
20.(本小题满分16分)
设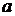 为实数,函数
为实数,函数 .
.
(1) 若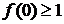 ,求
,求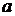 的取值范围;
的取值范围;
(2) 求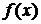 的最小值;
的最小值;
(3) 设函数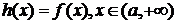 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式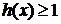 的解集.
的解集.
[解析](1)若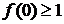 ,则
,则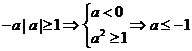
(2)当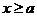 时,
时,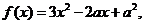

当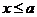 时,
时,
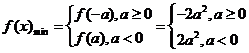
综上
(3) 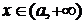 时,
时,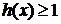 得
得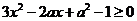 ,
,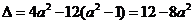
当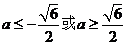 时,
时,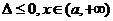 ;
;
当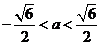 时,
时,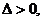 得
得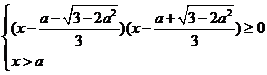
1)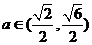 时,
时,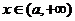
2)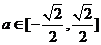 时,
时,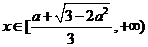
3)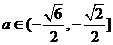 时,
时,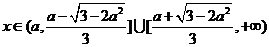
19.(本小题满分16分)
按照某学者的理论,假设一个人生产某产品单件成本为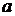 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为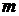 元,则他的满意度为
元,则他的满意度为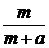 ;如果他买进该产品的单价为
;如果他买进该产品的单价为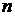 元,则他的满意度为
元,则他的满意度为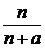 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为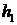 和
和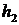 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为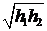 .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为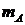 元和
元和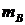 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为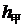 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为
(1) 求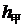 和
和 关于
关于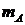 、
、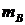 的表达式;当
的表达式;当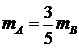 时,求证:
时,求证: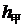 =
= ;
;
(2) 设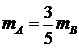 ,当
,当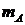 、
、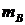 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
(3) 记(2)中最大的综合满意度为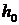 ,试问能否适当选取
,试问能否适当选取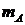 、
、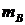 的值,使得
的值,使得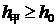 和
和 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
(4) 求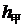 和
和 关于
关于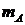 、
、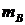 的表达式;当
的表达式;当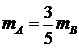 时,求证:
时,求证: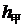 =
= ;
;
(5) 设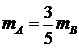 ,当
,当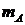 、
、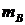 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
(6) 记(2)中最大的综合满意度为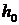 ,试问能否适当选取
,试问能否适当选取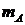 、
、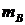 的值,使得
的值,使得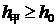 和
和 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
[解析](1)
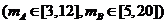
当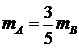 时,
时,
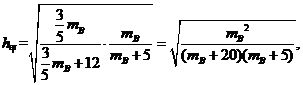
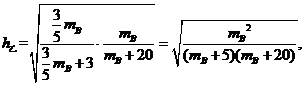
显然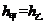
(2)当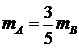 时,
时,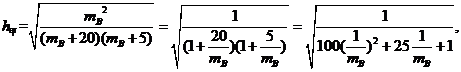
由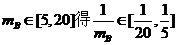 ,故当
,故当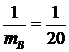 即
即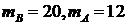 时,甲乙两人同时取到最大的综合满意度为
时,甲乙两人同时取到最大的综合满意度为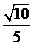
18.(本小题满分16分)
在平面直角坐标系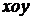 中,已知圆
中,已知圆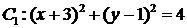 和圆
和圆
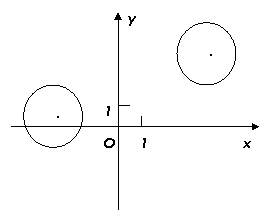
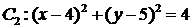
(1)若直线 过点
过点 ,且被圆
,且被圆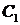 截得的弦长为
截得的弦长为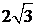 ,求直线
,求直线 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂的直线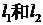 ,它们分别与圆
,它们分别与圆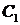 和圆
和圆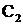 相交,且直线
相交,且直线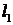 被圆
被圆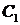 截得的弦长与直线
截得的弦长与直线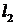 被圆
被圆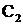 截得的弦长相等,试求所有满足条件的点P的坐标.
截得的弦长相等,试求所有满足条件的点P的坐标.
[解析](1) 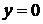 或
或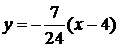 ,
,
(2)P在以C1C2的中垂线上,且与C1、C2等腰直角三角形,利用几何关系计算可得点P坐标为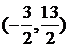 或
或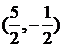 。
。
17.(本小题满分14分)
设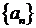 是公差不为零的等差数列,
是公差不为零的等差数列,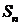 为其前
为其前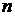 项和,满足
项和,满足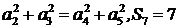
(1)求数列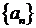 的通项公式及前
的通项公式及前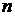 项和
项和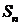 ;
;
(2)试求所有的正整数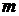 ,使得
,使得 为数列
为数列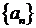 中的项.
中的项.
(1)设公差为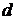 ,则
,则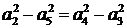 ,由性质得
,由性质得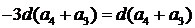 ,因为
,因为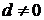 ,所[解析]以
,所[解析]以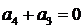 ,即
,即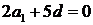 ,又由
,又由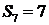 得
得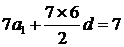 ,解得
,解得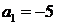 ,
,
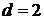 所以
所以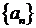 的通项公式为
的通项公式为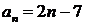 ,前
,前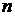 项和
项和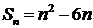 。
。
(2)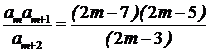 ,令
,令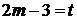 ,
,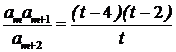
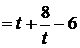 ,
,
因为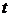 是奇数,所以
是奇数,所以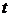 可取的值为
可取的值为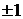 ,当
,当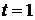 ,
,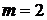 时,
时,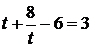 ,
,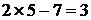 ,是数列
,是数列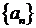 中的项;
中的项;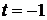 ,
,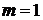 时,
时,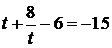 ,数列
,数列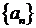 中的最小项是
中的最小项是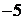 ,不符合。
,不符合。
所以满足条件的正整数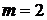 。
。
16.(本小题满分14分)
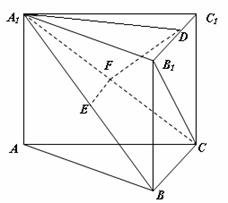
如图,在直三棱柱 中,
中,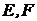 分别是
分别是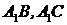 的中点,点
的中点,点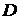 在
在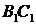 上,
上,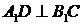
求证:(1)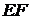 ∥
∥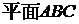
 (2)
(2)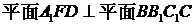
[解析]证明:(1)因为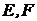 分别是
分别是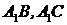 的中点,所以
的中点,所以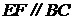 ,又
,又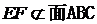 ,
,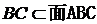 ,所以
,所以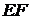 ∥
∥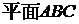 ;
;
(2)因为直三棱柱 ,所以
,所以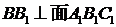 ,
,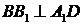 ,又
,又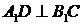 ,所以
,所以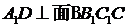 ,又
,又 ,所以
,所以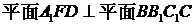 。
。
15.(本小题满分14分)
设向量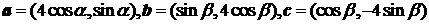
(1)若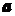 与
与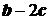 垂直,求
垂直,求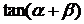 的值;
的值;
(2)求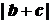 的最大值;
的最大值;
(3)若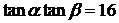 ,求证:
,求证: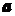 ∥
∥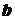 .
.
[解析]由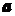 与
与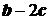 垂直,
垂直,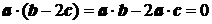 ,
,
即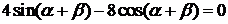 ,
,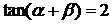 ;
;

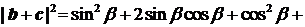
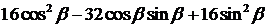
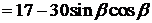
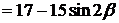 ,最大值为32,所以
,最大值为32,所以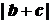 的最大值为
的最大值为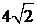 。
。
由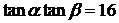 得
得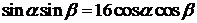 ,即
,即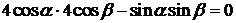 ,
,
所以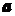 ∥
∥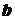 .
.
14.设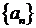 是公比为
是公比为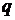 的等比数列,
的等比数列,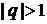 ,令
,令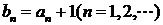 若数列
若数列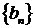 有连续四项在集合
有连续四项在集合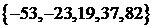 中,则
中,则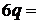 ★ .
★ .
[答案]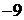
[解析]将各数按照绝对值从小到大排列,各数减1,观察即可得解.
13.如图,在平面直角坐标系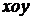 中,
中,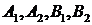 为椭圆
为椭圆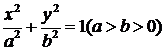 的四个顶点,
的四个顶点,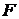 为其右焦点,直线
为其右焦点,直线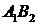 与直线
与直线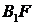 相交于点T,线段
相交于点T,线段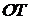 与椭圆的交点
与椭圆的交点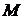 恰为线段
恰为线段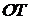 的中点,则该椭圆的离心率为 ★ .
的中点,则该椭圆的离心率为 ★ .
[答案]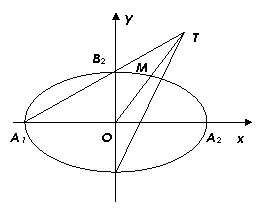
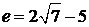
[解析]用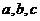 表示交点T,得出M坐标,代入椭圆方程即可转化解得离心率.
表示交点T,得出M坐标,代入椭圆方程即可转化解得离心率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com