
28.(2009宁夏海南卷文)(本小题满分12分) 

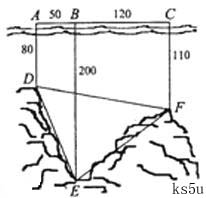 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知 ,
,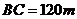 ,于A处测得水深
,于A处测得水深 ,于B处测得水深
,于B处测得水深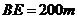 ,于C处测得水深
,于C处测得水深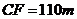 ,求∠DEF的余弦值。
,求∠DEF的余弦值。


(17) 解:
作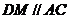 交BE于N,交CF于M.21世纪教育网
交BE于N,交CF于M.21世纪教育网


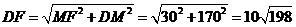 ,
, 

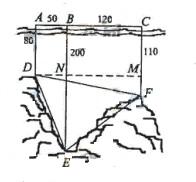
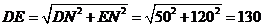
 ,
,
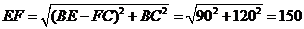 . ......6分
. ......6分 

在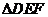 中,由余弦定理,
中,由余弦定理,
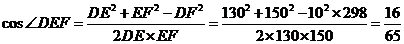 . ......12分
. ......12分
27.(2009湖北卷文)(本小题满分12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且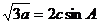
(Ⅰ)确定角C的大小:


(Ⅱ)若c=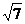 ,且△ABC的面积为
,且△ABC的面积为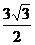
 ,求a+b的值。
,求a+b的值。
解(1)由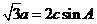 及正弦定理得,
及正弦定理得,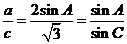 21世纪教育网
21世纪教育网


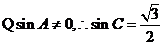
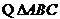 是锐角三角形,
是锐角三角形,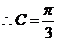
(2)解法1: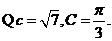 由面积公式得
由面积公式得
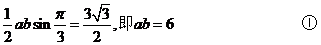
由余弦定理得21世纪教育网



由②变形得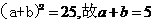
解法2:前同解法1,联立①、②得
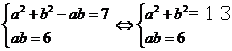
消去b并整理得 解得
解得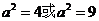
所以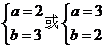 故
故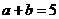 21世纪教育网
21世纪教育网


26.(2009四川卷文)(本小题满分12分)
在 中,
中,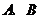 为锐角,角
为锐角,角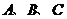 所对的边分别为
所对的边分别为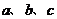 ,且
,且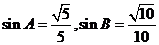
(I)求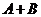 的值;
的值;
(II)若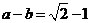 ,求
,求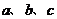 的值。21世纪教育网
的值。21世纪教育网 

[解析](I)∵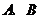 为锐角,
为锐角,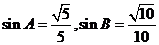
∴ 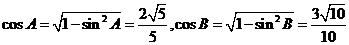
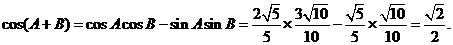
∵ 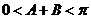
∴ 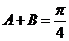 …………………………………………6分
…………………………………………6分
(II)由(I)知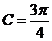 ,∴
,∴ 
由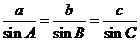 得
得
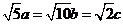 ,即
,即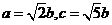
又∵ 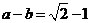 21世纪教育网
21世纪教育网 

∴ 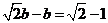 ∴
∴ 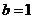
∴ 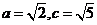 …………………………………………12分
…………………………………………12分
17、解(1)由最低点为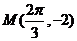 得A=2.
得A=2.
由x轴上相邻的两个交点之间的距离为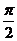 得
得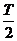 =
=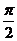 ,即
,即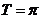 ,
,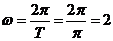
由点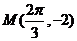 在图像上的
在图像上的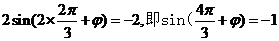
故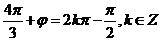
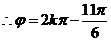 21世纪教育网
21世纪教育网 

又
(2)

当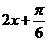 =
=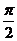 ,即
,即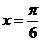 时,
时,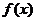 取得最大值2;当
取得最大值2;当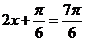
即 时,
时,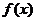 取得最小值-1,故
取得最小值-1,故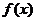 的值域为[-1,2] 21世纪教育网
的值域为[-1,2] 21世纪教育网 

25.(2009陕西卷理)(本小题满分12分)
已知函数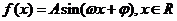 (其中
(其中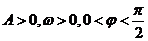 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为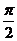 ,且图象上一个最低点为
,且图象上一个最低点为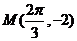 .
.
(Ⅰ)求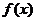 的解析式;(Ⅱ)当
的解析式;(Ⅱ)当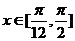 ,求
,求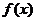 的值域.
的值域.
24.(2009陕西卷文)(本小题满分12分)
已知函数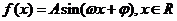 (其中
(其中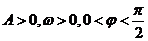 )的周期为
)的周期为 ,且图象上一个最低点为
,且图象上一个最低点为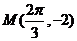 .
.
(Ⅰ)求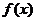 的解析式;(Ⅱ)当
的解析式;(Ⅱ)当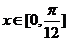 ,求
,求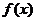 的最值.
的最值.
解析:(1)由最低点为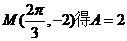 由
由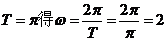
由点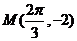 在图像上得
在图像上得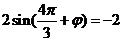 即
即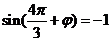
所以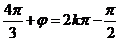 故
故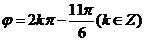
又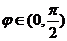 ,所以
,所以 所以
所以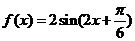
(Ⅱ)因为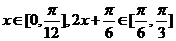
所以当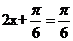 时,即x=0时,f(x)取得最小值1;
时,即x=0时,f(x)取得最小值1;
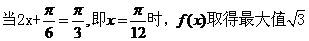 ;
;
23.(2009宁夏海南卷理)(本小题满分12分)
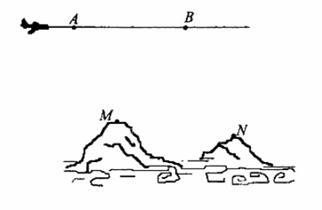
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。
(17) 解:
方案一:①需要测量的数据有:A
点到M,N点的俯角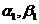 ;B点到M,
;B点到M,
N的俯角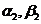 ;A,B的距离 d (如图所示) .
……….3分
;A,B的距离 d (如图所示) .
……….3分
②第一步:计算AM . 由正弦定理 ;
;
第二步:计算AN . 由正弦定理 ;
;
第三步:计算MN. 由余弦定理 .
.
方案二:①需要测量的数据有:
A点到M,N点的俯角 ,
,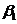 ;B点到M,N点的府角
;B点到M,N点的府角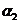 ,
, ;A,B的距离 d (如图所示).
;A,B的距离 d (如图所示).
②第一步:计算BM . 由正弦定理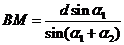 ;
;
第二步:计算BN . 由正弦定理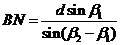 ;
;
第三步:计算MN . 由余弦定理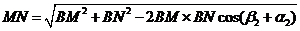
22.(2009辽宁卷理)(本小题满分12分)
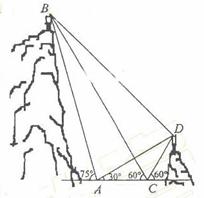
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为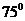 ,
,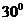 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,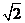
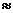 1.414,
1.414,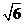
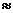 2.449)
2.449) 

(17)解:
在△ABC中,∠DAC=30°, ∠ADC=60°-∠DAC=30,
所以CD=AC=0.1 又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA, ……5分
在△ABC中,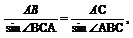
即AB=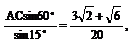
因此,BD=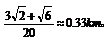
故B,D的距离约为0.33km。 ……12分
21.(2009辽宁卷文)(本小题满分12分)
 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为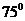 ,
,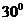 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,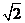
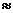 1.414,
1.414,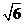
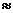 2.449)
2.449) 

(18)解:
在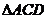 中,
中, =30°,
=30°,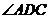 =60°-
=60°- =30°,
=30°,
所以CD=AC=0.1
又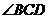 =180°-60°-60°=60°,
=180°-60°-60°=60°,
故CB是 底边AD的中垂线,所以BD=BA
5分
底边AD的中垂线,所以BD=BA
5分
在 中,
中,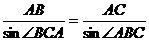 ,
, 

即AB=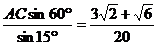
因此,
故B、D的距离约为0.33km。 12分
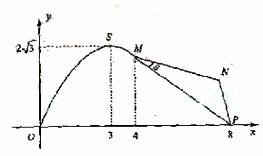
18.本小题主要考查三角函数的图象与性质、解三角形等基础知识,考查运算求解能力以及应用数学知识分析和解决实际问题的能力,考查化归与转化思想、数形结合思想,
解法一
(Ⅰ)依题意,有 ,
,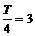 ,又
,又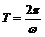 ,
,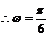 。
。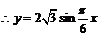
当  是,
是,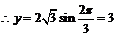
 又
又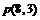
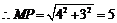
(Ⅱ)在△MNP中∠MNP=120°,MP=5,
设∠PMN=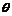 ,则0°<
,则0°<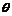 <60°
<60°
由正弦定理得
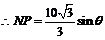 ,
,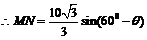
故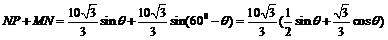
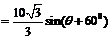
 0°<
0°<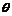 <60°,
<60°, 当
当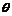 =30°时,折线段赛道MNP最长
=30°时,折线段赛道MNP最长
亦即,将∠PMN设计为30°时,折线段道MNP最长
解法二:
(Ⅰ)同解法一
(Ⅱ)在△MNP中,∠MNP=120°,MP=5,
由余弦定理得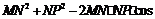 ∠MNP=
∠MNP=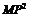
即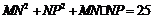
故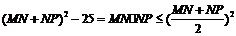
从而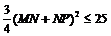 ,即
,即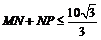
当且仅当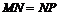 时,折线段道MNP最长
时,折线段道MNP最长
注:本题第(Ⅱ)问答案及其呈现方式均不唯一,除了解法一、解法二给出的两种设计方式,还可以设计为:①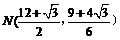 ;②
;②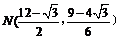 ;③点N在线段MP的垂直平分线上等
;③点N在线段MP的垂直平分线上等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com