5、在轻绳的两端各栓一个小球，一人用手拿者上端的小球站在3层楼阳台上，放手后让小球自由下落，两小球相继落地的时间差为T，如果站在4层楼的阳台上，同样放手让小球自由下落，则两小球相继落地时间差将　　 (　　　　 )

A 不变 　　　　　B 变大　 　　　　　C 变小　　 　　　　D 无法判断

解析：两小球都是自由落体运动，可在一v-t图象中作出速度随时间的关系曲线，如图所示，设人在3楼阳台上释放小球后，两球落地时间差为△t₁，图中阴影部分面积为△h，若人在4楼阳台上释放小球后，两球落地时间差△t₂，要保证阴影部分面积也是△h；从图中可以看出一定有△t₂〈△t₁

答案：C

4、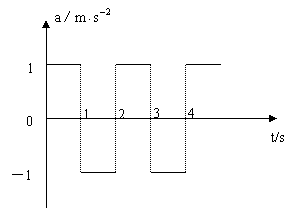汽车甲沿着平直的公路以速度v₀做匀速直线运动，当它路过某处的同时，该处有一辆汽车乙开始做初速度为零的匀加速运动去追赶甲车，根据上述的已知条件(　　 )

A.　　 可求出乙车追上甲车时乙车的速度

B.　　 可求出乙车追上甲车时乙车所走的路程

C.　　 可求出乙车从开始起动到追上甲车时所用的时间

D.　　 不能求出上述三者中任何一个

分析：题中涉及到2个相关物体运动问题，分析出2个物体各作什么运动，并尽力找到两者相关的物理条件是解决这类问题的关键，通常可以从位移关系、速度关系或者时间关系等方面去分析。

解析：根据题意，从汽车乙开始追赶汽车甲直到追上，两者运动距离相等，即s_甲=

=s_乙=s，经历时间t_甲=t_乙=t.

那么，根据匀速直线运动公式对甲应有：

根据匀加速直线运动公式对乙有：，及

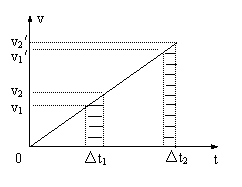
由前2式相除可得at=2v₀，代入后式得v_t=2v₀，这就说明根据已知条件可求出乙车追上甲车时乙车的速度应为2v₀。因a不知，无法求出路程和时间，如果我们采取作v－t图线的方法，则上述结论就比较容易通过图线看出。图中当乙车追上甲车时，路程应相等，即从图中图线上看面积s_甲和s_乙，显然三角形高vt等于长方形高v₀的2倍，由于加速度a未知，乙图斜率不定，a越小，t越大，s也越大，也就是追赶时间和路程就越大。

答案：A

3、汽车原来以速度v匀速行驶,刹车后加速度大小为a,做匀减速运动,则t秒后其位移为(　　 )

A　 　　B　 　　　　C 　　D　 无法确定

解析:汽车初速度为v，以加速度a作匀减速运动。速度减到零后停止运动，设其运动的时间t^，=。当t≤t^，时，汽车的位移为s=；如果t＞t^，，汽车在t^，时已停止运动，其位移只能用公式v²=2as计算，s=

答案：D

2、 一个物体在做初速度为零的匀加速直线运动，已知它在第一个△t时间内的位移为s，若 △t未知，则可求出　　　　　　　 (　 )

A．　 第一个△t时间内的平均速度

B．　 第n个△t时间内的位移

C．　 n△t时间的位移

D．　 物体的加速度　

解析：因=，而△t未知，所以不能求出，故A错.因有，(2n-1)s，故B正确；又s∝t²　 所以⁼n²，所以s_n=n2s，故C正确；因a=，尽管△s=s_n-s_n-1可求，但△t未知，所以A求不出，D错.

答案：B、C

1、 下列关于所描述的运动中，可能的是　　　 (　　　　 )

A 速度变化很大，加速度很小

B 速度变化的方向为正，加速度方向为负

C 速度变化越来越快，加速度越来越小

D 速度越来越大，加速度越来越小

解析：由a=△v/△t知，即使△v很大，如果△t足够长，a可以很小，故A正确。速度变化的方向即△v的方向，与a方向一定相同，故B错。加速度是描述速度变化快慢的物理量，速度变化快，加速度一定大。故C错。加速度的大小在数值上等于单位时间内速度的改变量，与速度大小无关，故D正确。

答案：A、D

例题1.一物体做匀变速直线运动，某时刻速度大小为4m/s，1s后速度的大小变为10m/s，在这1s内该物体的　　　　　　　　　　 (　　　 )

A.位移的大小可能小于4m

B.位移的大小可能大于10m

C.加速度的大小可能小于4m/s

D.加速度的大小可能大于10m/s

析：同向时

　　 反向时

式中负号表示方向跟规定正方向相反

答案：A、D

例题2：两木块自左向右运动，现用高速摄影机在同一底片上多次曝光，记录下木快每次曝光时的位置，如图所示，连续两次曝光的时间间隔是相等的，由图可知　 (　　　 )

A　 在时刻t₂以及时刻t₅两木块速度相同

B　 在时刻t1两木块速度相同

C　 在时刻t₃和时刻t₄之间某瞬间两木块速度相同

D　 在时刻t₄和时刻t₅之间某瞬间两木块速度相同

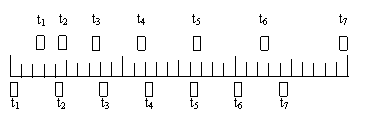解析：首先由图看出：上边那个物体相邻相等时间内的位移之差为恒量，可以判定其做匀变速直线运动；下边那个物体很明显地是做匀速直线运动。由于t₂及t₃时刻两物体位置相同，说明这段时间内它们的位移相等，因此其中间时刻的即时速度相等，这个中间时刻显然在t₃、t₄之间

答案：C

例题3　 一跳水运动员从离水面10m高的平台上跃起，举双臂直立身体离开台面，此时中心位于从手到脚全长的中点，跃起后重心升高0.45m达到最高点，落水时身体竖直，手先入水(在此过程中运动员水平方向的运动忽略不计)从离开跳台到手触水面，他可用于完成空中动作的时间是多少？(g取10m/s²结果保留两位数字)

解析：根据题意计算时，可以把运动员的全部质量集中在重心的一个质点，且忽略其水平方向的运动，因此运动员做的是竖直上抛运动，由可求出刚离开台面时的速度，由题意知整个过程运动员的位移为－10m(以向上为正方向)，由得：

－10=3t－5t²

解得：t≈1.7s

思考：把整个过程分为上升阶段和下降阶段来解，可以吗？

例题4.如图所示，有若干相同的小钢球，从斜面上的某一位置每隔0.1s释放一颗，在连续释放若干颗钢球后对斜面上正在滚动的若干小球摄下照片如图，测得AB=15cm，BC=20cm，试求：

(1)　　　 拍照时B球的速度；

(2)　　　 A球上面还有几颗正在滚动的钢球

解析：拍摄得到的小球的照片中，A、B、C、D…各小球的位置，正是首先释放的某球每隔0.1s所在的位置.这样就把本题转换成一个物体在斜面上做初速度为零的匀加速运动的问题了。求拍摄时B球的速度就是求首先释放的那个球运动到B处的速度；求A球上面还有几个正在滚动的小球变换为首先释放的那个小球运动到A处经过了几个时间间隔(0.1s)

(1)A、B、C、D四个小球的运动时间相差△T=0.1s

V_B==m/s=1.75m/s

(2)由△s=a△T²得：

a=m/s²==5m/s²

例5：火车A以速度v₁匀速行驶，司机发现正前方同一轨道上相距s处有另一火车B沿同方向以速度v₂(对地，且v₂〈v₁〉做匀速运动，A车司机立即以加速度(绝对值)a紧急刹车，为使两车不相撞，a应满足什么条件？

分析：后车刹车做匀减速运动，当后车运动到与前车车尾即将相遇时，如后车车速已降到等于甚至小于前车车速，则两车就不会相撞，故取s_后=s+s_前和v_后≤v_前求解

解法一：取取上述分析过程的临界状态，则有

v₁t－a₀t²＝s+v₂t

v₁－a₀t = v₂

a₀ =

所以当a≥　 时，两车便不会相撞。

法二：如果后车追上前车恰好发生相撞，则

v₁t－at² ＝ s +v₂t

上式整理后可写成有关t的一元二次方程，即

at²+(v₂－v₁)t+s ＝ 0

取判别式△〈0，则t无实数解，即不存在发生两车相撞时间t。△≥0，则有

(v₂－v₁)²≥4(a)s

得a≤

为避免两车相撞，故a≥

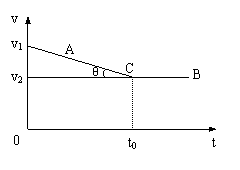
法三：运用v-t图象进行分析，设从某时刻起后车开始以绝对值为a的加速度开始刹车，取该时刻为t=0，则A、B两车的v-t图线如图所示。图中由v₁ 、v₂、C三点组成的三角形面积值即为A、B两车位移之差(s_后－s_前)=s，tanθ即为后车A减速的加速度绝对值a₀。因此有

(v₁－v₂)=s

所以 tanθ=a₀=

若两车不相撞需a≥a₀=

21. (I)证： 三棱柱中，　　　　　

　　 又平面，且平面， 平面　　　　　　　　　　　　　　　　

　　 (II)证： 三棱柱中， 中

　　 是等腰三角形　 ，E是等腰底边的中点，

　　 　又依条件知 且

　　 由①，②，③得平面EDB　　　　　　　　

　　 (III)解： 平面， 且不平行，故延长，ED后必相交， 设交点为E，连接EF，如下图是所求的二面角　　　　　　　

　　 依条件易证明　 为中点， A为中点

　　 即　　　　 又平面EFB， 　是所求的二面角的平面角 　　 ， E为等腰直角三角形底边中点，

　　 故所求的二面角的大小为　　　　　　

22　 证明　 (1)当n=1时，4^2×1+1+3¹⁺²=91能被13整除

(2)假设当n=k时，4^2k+1+3^k+2能被13整除，则当n=k+1时，

4^2(k+1)+1+3^k+3=4^2k+1·4²+3^k+2·3－4^2k+1·3+4^2k+1·3

=4^2k+1·13+3·(4^2k+1+3^k+2?)

∵4^2k+1·13能被13整除，4^2k+1+3^k+2能被13整除

∴当n=k+1时也成立　

由①②知，当n∈N^*时，4²ⁿ⁺¹+3ⁿ⁺²能被13整除　

20. 解：(I)设“甲队以3：0获胜”为事件A，则　　　

　　 (II)设“甲队获得总冠军”为事件B，

　　 则事件B包括以下结果：3：0；3：1；3：2三种情况

　　 若以3：0胜，则；　　　　　　　　　　　　　　　　

　　 若以3：1胜，则　　　　　　　　　　　　　　　

　　 若以3：2胜，则　　　　　　　　　　　　　

所以，甲队获得总冠军的概率为

19. 解：(Ⅰ)证明：CD//C₁B₁，又BD=BC=B₁C₁，∴ 四边形BDB₁C₁是平行四边形，

∴BC₁//DB₁.又DB₁平面AB₁D，BC₁平面AB₁D，∴直线BC₁//平面AB₁D.

(Ⅱ)解：过B作BE⊥AD于E，连结EB₁，∵B₁B⊥平面ABD，∴B₁E⊥AD ，

∴∠B₁EB是二面角B₁-AD-B的平面角，∵BD=BC=AB，∴E是AD的中点， 在Rt△B₁BE中，　 ∴∠B₁EB=60°。即二面角B₁-AD-B的大小为60°

21、直三棱柱ABC-A₁B₁C₁中，，E是A₁C的中点，且交AC于D，。(I)证明：平面；(II)证明：平面；

　 (III)求平面与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。

22　 用数学归纳法证明4+3ⁿ⁺²能被13整除，其中n∈N^*