
24.(19分)
解:小滑块运动到位置 时速度为v1,由动能定理有:
时速度为v1,由动能定理有:
 ①
①
v1=
 ②
②
说明:①式2分,②式1分。
(2)由题意可知,电场方向如图,若小滑块能通过位置p,则小滑块可沿挡板运动且通过位置p5,设小滑块在位置p的速度为v,受到的挡板的弹力为N,匀强电场的电场强度为E,由动能定理有: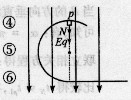
 =
= ③
③
当滑块在位置p时,由牛顿第二定律有:N+Eq=m ④
④
由题意有:N 0
⑤
0
⑤
由以上三式可得:E ⑥
⑥
E的取值范围:0< E ⑦
⑦
说明:③④⑤⑥式各2分,⑦式1分
(3)设线圈产生的电动势为E1,其电阻为R,平行板电容器两端的电压为U,t时间内磁感应强度的变化量为 B,得:U=Ed
⑧
B,得:U=Ed
⑧
由法拉第电磁感应定律得E1=n ⑨
⑨
由全电路的欧姆定律得E1=I(R+2R) ⑩
U=2RI
 经过时间t,磁感应强度变化量的取值范围:0<
经过时间t,磁感应强度变化量的取值范围:0<
说明:
24.(09四川卷)(19分)
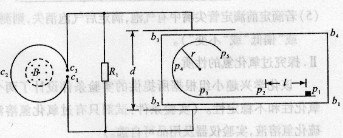
如图所示,直线形挡板p1p2p3与半径为r的圆弧形挡板p3p4p5平滑连接并安装在水平台面b1b2b3b4上,挡板与台面均固定不动。线圈c1c2c3的匝数为n,其端点c1、c3通过导线分别与电阻R1和平行板电容器相连,电容器两极板间的距离为d,电阻R1的阻值是线圈c1c2c3阻值的2倍,其余电阻不计,线圈c1c2c3内有一面积为S、方向垂直于线圈平面向上的匀强磁场,磁场的磁感应强度B随时间均匀增大。质量为m的小滑块带正电,电荷量始终保持为q,在水平台面上以初速度v0从p1位置出发,沿挡板运动并通过p5位置。若电容器两板间的电场为匀强电场,p1、p2在电场外,间距为l,其间小滑块与台面的动摩擦因数为μ,其余部分的摩擦不计,重力加速度为g.
 求:
求:
(1) 小滑块通过p2位置时的速度大小。
(2) 电容器两极板间电场强度的取值范围。
(3)经过时间t,磁感应强度变化量的取值范围。
16. (1)设匀强磁场的磁感应强度的大小为B。令圆弧 是自C点垂直于BC入射的电子在磁场中的运行轨道。电子所受到的磁场的作用力
是自C点垂直于BC入射的电子在磁场中的运行轨道。电子所受到的磁场的作用力

 应指向圆弧的圆心,因而磁场的方向应垂直于纸面向外。圆弧
应指向圆弧的圆心,因而磁场的方向应垂直于纸面向外。圆弧 的圆心在CB边或其延长线上。依题意,圆心在A、C连线的中垂线上,故B 点即为圆心,圆半径为
的圆心在CB边或其延长线上。依题意,圆心在A、C连线的中垂线上,故B 点即为圆心,圆半径为 按照牛顿定律有
按照牛顿定律有
联立①②式得
(2)由(1)中决定的磁感应强度的方向和大小,可知自 点垂直于
点垂直于 入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而,圆弧
入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而,圆弧 是所求的最小磁场区域的一个边界。
是所求的最小磁场区域的一个边界。
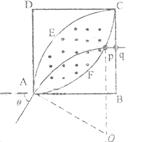
为了决定该磁场区域的另一边界,我们来考察射中A点的电子的速度方向与BA的延长线交角为 (不妨设
(不妨设 )的情形。该电子的运动轨迹
)的情形。该电子的运动轨迹 如右图所示。
如右图所示。
图中,圆 的圆心为O,pq垂直于BC边 ,由③式知,圆弧
的圆心为O,pq垂直于BC边 ,由③式知,圆弧 的半径仍为
的半径仍为 ,在D为原点、DC为x轴,AD为
,在D为原点、DC为x轴,AD为 轴的坐标系中,P点的坐标
轴的坐标系中,P点的坐标 为
为

这意味着,在范围 内,p点形成以D为圆心、
内,p点形成以D为圆心、 为半径的四分之一圆周
为半径的四分之一圆周 ,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界。
,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界。
因此,所求的最小匀强磁场区域时分别以 和
和 为圆心、
为圆心、 为半径的两个四分之一圆周
为半径的两个四分之一圆周 和
和 所围成的,其面积为
所围成的,其面积为
评分参考:本题10分。第(1)问4分,①至③式各1分;得出正确的磁场方向的,再给1分。第(2)问6分,得出“圆弧 是所求磁场区域的一个边界”的,给2分;得出所求磁场区域的另一个边界的,再给2分;⑥式2分。
是所求磁场区域的一个边界”的,给2分;得出所求磁场区域的另一个边界的,再给2分;⑥式2分。
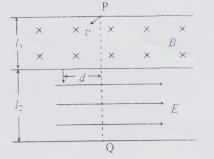
(09北京卷)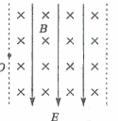 19.如图所示的虚线区域内,充满垂直于纸面向里的匀强磁场和竖直向下的匀强电场。一带电粒子a(不计重力)以一定的初速度由左边界的O点射入磁场、电场区域,恰好沿直线由区域右边界的O′点(图中未标出)穿出。若撤去该区域内的磁场而保留电场不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b
19.如图所示的虚线区域内,充满垂直于纸面向里的匀强磁场和竖直向下的匀强电场。一带电粒子a(不计重力)以一定的初速度由左边界的O点射入磁场、电场区域,恰好沿直线由区域右边界的O′点(图中未标出)穿出。若撤去该区域内的磁场而保留电场不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b
A.穿出位置一定在O′点下方
B.穿出位置一定在O′点上方
C.运动时,在电场中的电势能一定减小
D.在电场中运动时,动能一定减小
[解析]a粒子要在电场、磁场的复合场区内做直线运动,则该粒子一定做匀速直线运动,故对粒子a有:Bqv=Eq 即只要满足E =Bv无论粒子带正电还是负电,粒子都可以沿直线穿出复合场区,当撤去磁场只保留电场时,粒子b由于电性不确定,故无法判断从O’点的上方或下方穿出,故AB错误;粒子b在穿过电场区的过程中必然受到电场力的作用而做类似于平抛的运动,电场力做正功,其电势能减小,动能增大,故C项正确D项错误。
[答案]C
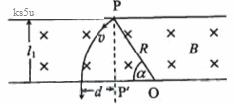
 (09全国Ⅱ卷)25.如图,在的两个相邻的条形区域分别有匀强磁场和匀强电磁场与向垂直于纸面向里,电场方向与电,磁场匀界线平行左右一带正电荷的粒子以速率磁场区域上边界的P点斜射入磁场,然后以垂直于电,磁场分界线的方向进入电场,最生从电场边界上的Q点射出,已知PQ垂直于电场方向粒子轨迹与电,磁场分界线的交点到PQ的距离为d不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比
(09全国Ⅱ卷)25.如图,在的两个相邻的条形区域分别有匀强磁场和匀强电磁场与向垂直于纸面向里,电场方向与电,磁场匀界线平行左右一带正电荷的粒子以速率磁场区域上边界的P点斜射入磁场,然后以垂直于电,磁场分界线的方向进入电场,最生从电场边界上的Q点射出,已知PQ垂直于电场方向粒子轨迹与电,磁场分界线的交点到PQ的距离为d不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比

 答案
答案
 [解析]本题考查带电粒子在有界磁场中的运动.
[解析]本题考查带电粒子在有界磁场中的运动.
 粒子在磁场中做匀速圆周运动,如图所示.由于粒子在分界线处的速度与分界线垂直,圆心O应在分界线上,OP长度即为粒子运动的圆弧的半径R.由几何关系得
粒子在磁场中做匀速圆周运动,如图所示.由于粒子在分界线处的速度与分界线垂直,圆心O应在分界线上,OP长度即为粒子运动的圆弧的半径R.由几何关系得
 ………①
………①
 设粒子的质量和所带正电荷分别为m和q,由洛仑兹力公式和牛顿第二定律得
设粒子的质量和所带正电荷分别为m和q,由洛仑兹力公式和牛顿第二定律得


 ……………②
……………②

 设
设 为虚线与分界线的交点,
为虚线与分界线的交点, ,则粒子在磁场中的运动时间为
,则粒子在磁场中的运动时间为 ……③
……③
 式中有
式中有 ………④粒子进入电场后做类平抛运动,其初速度为v,方向垂直于电场.设粒子的加速度大小为a,由牛顿第二定律得
………④粒子进入电场后做类平抛运动,其初速度为v,方向垂直于电场.设粒子的加速度大小为a,由牛顿第二定律得 …………⑤
…………⑤
 由运动学公式有
由运动学公式有 ……⑥
……⑥
 ………⑦
………⑦
 由①②⑤⑥⑦式得
由①②⑤⑥⑦式得 …………⑧
…………⑧
 由①③④⑦式得
由①③④⑦式得
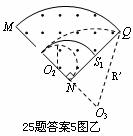
(09重庆卷)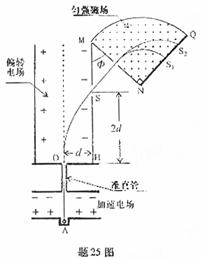 25.(19分)如题25图,离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管,垂直射入匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过一段匀速直线运动,垂直于边界MN进入磁感应强度为B的匀强磁场。已知HO=d,HS=2d,
25.(19分)如题25图,离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管,垂直射入匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过一段匀速直线运动,垂直于边界MN进入磁感应强度为B的匀强磁场。已知HO=d,HS=2d, =90°。(忽略粒子所受重力)
=90°。(忽略粒子所受重力)
(1)求偏转电场场强E0的大小以及HM与MN的夹角 ;
;
(2)求质量为m的离子在磁场中做圆周运动的半径;
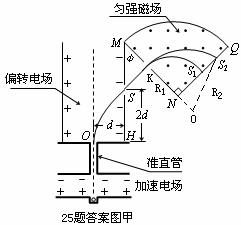
(3)若质量为4m的离子垂直打在NQ的中点 处,质量为16m的离子打在
处,质量为16m的离子打在 处。求
处。求 和
和 之间的距离以及能打在NQ上的正离子的质量范围。
之间的距离以及能打在NQ上的正离子的质量范围。
解析:
(1)
正离子被电压为U0的加速电场加速后速度设为V1,设
对正离子,应用动能定理有eU0= mV12,
mV12,
正离子垂直射入匀强偏转电场,作类平抛运动
 受到电场力F=qE0、产生的加速度为a=
受到电场力F=qE0、产生的加速度为a= ,即a=
,即a= ,
,
垂直电场方向匀速运动,有2d=V1t,
沿场强方向:Y= at2,
at2,
联立解得E0=
又tanφ= ,解得φ=45°;
,解得φ=45°;
(2)
 正离子进入磁场时的速度大小为V2=
正离子进入磁场时的速度大小为V2= ,
,
解得V2=
正离子在匀强磁场中作匀速圆周运动,由洛仑兹力提供向心力,qV2B= ,
,
解得离子在磁场中做圆周运动的半径R=2 ;
;
(3)根据R=2 可知,
可知,
质量为4m的离子在磁场中的运动打在S1,运动半径为R1=2 ,
,
质量为16m的离子在磁场中的运动打在S2,运动半径为R2=2 ,
,
又ON=R2-R1,
由几何关系可知S1和S2之间的距离ΔS= -R1,
-R1,
联立解得ΔS=4( -)
-) ;
;
由R′2=(2 R1)2+(
R′-R1)2解得R′= R1,
R1,
再根据 R1<R<
R1<R< R1,
R1,
解得m<mx<25m。
22.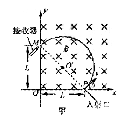
 (20分)
(20分)
 (1)设粒子在磁场中的运动半径为r。如图甲,依题意M、P连线即为该粒子在磁场中作匀速圆周运动的直径,由几何关系得
(1)设粒子在磁场中的运动半径为r。如图甲,依题意M、P连线即为该粒子在磁场中作匀速圆周运动的直径,由几何关系得

 ①
①
 由洛伦兹力提供粒子在磁场中作匀速圆周运动的向心力,可得
由洛伦兹力提供粒子在磁场中作匀速圆周运动的向心力,可得
 ②
②
联立①②并代入数据得 =4.9×
=4.9× C/kg(或5.0×
C/kg(或5.0× C/kg)
③
C/kg)
③
(2)设所加电场的场强大小为E。如图乙,当例子经过Q点时,速度沿y轴正方向,依题意,在此时加入沿x轴正方向的匀强电场,电场力与此时洛伦兹力平衡,则有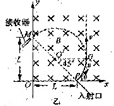
 ④
④
代入数据得
 ⑤
⑤
所加电场的长枪方向沿x轴正方向。由几何关系可知,圆弧PQ所对应的圆心角为45°,设带点粒子做匀速圆周运动的周期为T,所求时间为t,则有
 ⑥
⑥
 ⑦
⑦
联立①⑥⑦并代入数据得  ⑧
⑧
(3)如图丙,所求的最小矩形是 ,该区域面积
,该区域面积
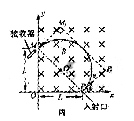
 ⑨
⑨
联立①⑨并代入数据得 
矩形如图丙中 (虚线)
(虚线)
(09 海南卷)
海南卷)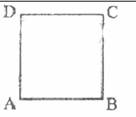 16.如图,ABCD是边长为
16.如图,ABCD是边长为 的正方形。质量为
的正方形。质量为 、电荷量为
、电荷量为 的电子以大小为
的电子以大小为 的初速度沿纸面垂直于BC变射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力,求:
的初速度沿纸面垂直于BC变射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力,求:
(1)次匀强磁场区域中磁感应强度的方向和大小;
(2)此匀强磁场区域的最小面积。
25.(09宁夏卷)(18分)如图所示,在第一象限有一均强电场,场强大小为E,方向与y轴平行;在x轴下方有一均强磁场,磁场方向与纸面垂直。一质量为m、电荷量为-q(q>0)的粒子以平行于x轴的速度从y轴上的P点处射入电场,在x轴上的Q点处进入磁场,并从坐标原点O离开磁场。粒子在磁场中的运动轨迹与y轴交于M点。已知OP= ,
, 。不计重力。求
。不计重力。求
 (1)M点与坐标原点O间的距离;
(1)M点与坐标原点O间的距离;
(2)粒子从P点运动到M点所用的时间。
[解析] (1)带电粒子在电场中做类平抛运动,在
(1)带电粒子在电场中做类平抛运动,在 轴负方向上做初速度为零的匀加速运动,设加速度的大小为
轴负方向上做初速度为零的匀加速运动,设加速度的大小为 ;在
;在 轴正方向上做匀速直线运动,设速度为
轴正方向上做匀速直线运动,设速度为 ,粒子从P点运动到Q点所用的时间为
,粒子从P点运动到Q点所用的时间为 ,进入磁场时速度方向与
,进入磁场时速度方向与 轴正方向的夹角为
轴正方向的夹角为 ,则
,则
 ①
① 
 ②
② 
 ③
③
 其中
其中 。又有
。又有
 ④
④
 联立②③④式,得
联立②③④式,得

 因为
因为 点在圆周上,
点在圆周上, ,所以MQ为直径。从图中的几何关系可知。
,所以MQ为直径。从图中的几何关系可知。

 ⑥
⑥ 
 ⑦
⑦
 (2)设粒子在磁场中运动的速度为
(2)设粒子在磁场中运动的速度为 ,从Q到M点运动的时间为
,从Q到M点运动的时间为 ,
,
则有
 ⑧
⑧

 ⑨
⑨
 带电粒子自P点出发到M点所用的时间为
带电粒子自P点出发到M点所用的时间为 为
为
 ⑩
⑩
 联立①②③⑤⑥⑧⑨⑩式,并代入数据得
联立①②③⑤⑥⑧⑨⑩式,并代入数据得
 11
11
 (09福建卷)
(09福建卷) 22.(20分)
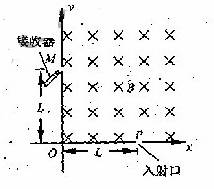
22.(20分) 图为可测定比荷的某装置的简化示意图,在第一象限区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B=2.0×10-3T,在X轴上距坐标原点L=0.50m的P处为离子的入射口,在Y上安放接收器,现将一带正电荷的粒子以v=3.5×104m/s的速率从P处射入磁场,若粒子在y轴上距坐标原点L=0.50m的M处被观测到,且运动轨迹半径恰好最小,设带电粒子的质量为m,电量为q,不记其重力。
图为可测定比荷的某装置的简化示意图,在第一象限区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B=2.0×10-3T,在X轴上距坐标原点L=0.50m的P处为离子的入射口,在Y上安放接收器,现将一带正电荷的粒子以v=3.5×104m/s的速率从P处射入磁场,若粒子在y轴上距坐标原点L=0.50m的M处被观测到,且运动轨迹半径恰好最小,设带电粒子的质量为m,电量为q,不记其重力。
 (1)求上述粒子的比荷
(1)求上述粒子的比荷 ;
;
 (2)如果在上述粒子运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其沿y轴正方向做匀速直线运动,求该匀强电场的场强大小和方向,并求出从粒子射入磁场开始计时经过多长时间加这个匀强电场;
(2)如果在上述粒子运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其沿y轴正方向做匀速直线运动,求该匀强电场的场强大小和方向,并求出从粒子射入磁场开始计时经过多长时间加这个匀强电场;
 (3)为了在M处观测到按题设条件运动的上述粒子,在第一象限内的磁场可以局限在一个矩形区域内,求此矩形磁场区域的最小面积,并在图中画出该矩形。
(3)为了在M处观测到按题设条件运动的上述粒子,在第一象限内的磁场可以局限在一个矩形区域内,求此矩形磁场区域的最小面积,并在图中画出该矩形。
26. [解析]设粒子的入射速度为v,第一次射出磁场的点为
[解析]设粒子的入射速度为v,第一次射出磁场的点为 ,与板碰撞后再次进入磁场的位置为
,与板碰撞后再次进入磁场的位置为 .粒子在磁场中运动的轨道半径为R,有
.粒子在磁场中运动的轨道半径为R,有 …⑴,粒子速率不变,每次进入磁场与射出磁场位置间距离
…⑴,粒子速率不变,每次进入磁场与射出磁场位置间距离 保持不变有
保持不变有
 …⑵,粒子射出磁场与下一次进入磁场位置间的距离
…⑵,粒子射出磁场与下一次进入磁场位置间的距离 始终不变,与
始终不变,与 相等.由图可以看出
相等.由图可以看出 ……⑶
……⑶
设粒子最终离开磁场时,与档板相碰n次(n=0、1、2、3…).若粒子能回到P点,由对称性,出射点的x坐标应为-a,即 ……⑷,由⑶⑷两式得
……⑷,由⑶⑷两式得 ……⑸
……⑸
若粒子与挡板发生碰撞,有 ……⑹联立⑶⑷⑹得n<3………⑺联立⑴⑵⑸得
……⑹联立⑶⑷⑹得n<3………⑺联立⑴⑵⑸得
 ………⑻把
………⑻把 代入⑻中得
代入⑻中得
 …………⑼
…………⑼
 …………⑾
…………⑾
 …………⑿
…………⑿
19.(09安徽卷) 右图是科学史上一张著名的实验照片,显示一个带电粒子在云室中穿过某种金属板运动的径迹。云室旋转在匀强磁场中,磁场方向垂直照片向里。云室中横放的金 属板对粒子的运动起阻碍作用。分析此径迹可知粒子
属板对粒子的运动起阻碍作用。分析此径迹可知粒子
A. 带正电,由下往上运动
B. 带正电,由上往下运动
C. 带负电,由上往下运动
D. 带负电,由下往上运动
 答案: A。
答案: A。
 解析:粒子穿过金属板后,速度变小,由半径公式
解析:粒子穿过金属板后,速度变小,由半径公式 可知,半径变小,粒子运动方向为由下向上;又由于洛仑兹力的方向指向圆心,由左手定则,粒子带正电。选A。
可知,半径变小,粒子运动方向为由下向上;又由于洛仑兹力的方向指向圆心,由左手定则,粒子带正电。选A。
(09安徽卷)
 20. 如图甲所示,一个电阻为R,面积为S的矩形导线框abcd,水平旋转在匀强磁场中,磁场的磁感应强度为B,方向与ad边垂直并与线框平面成450角,o、o’ 分别是ab和cd边的中点。现将线框右半边obco’ 绕oo’
逆时针900到图乙所示位置。在这一过程中,导线中通过的电荷量是
20. 如图甲所示,一个电阻为R,面积为S的矩形导线框abcd,水平旋转在匀强磁场中,磁场的磁感应强度为B,方向与ad边垂直并与线框平面成450角,o、o’ 分别是ab和cd边的中点。现将线框右半边obco’ 绕oo’
逆时针900到图乙所示位置。在这一过程中,导线中通过的电荷量是
A.  B.
B.
 C.
C.
 D.
0
D.
0
 答案:A
答案:A
 解析:对线框的右半边(obco′)未旋转时整个回路的磁通量
解析:对线框的右半边(obco′)未旋转时整个回路的磁通量
 对线框的右半边(obco′)旋转90o后,穿进跟穿出的磁通量相等,如右 图整个回路的磁通量
对线框的右半边(obco′)旋转90o后,穿进跟穿出的磁通量相等,如右 图整个回路的磁通量 。
。 。根据公式
。根据公式 。选A
。选A


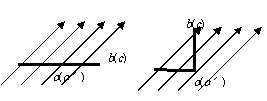
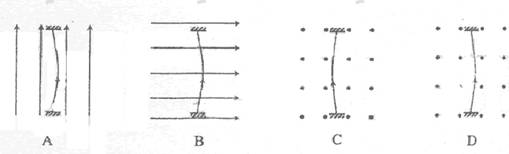
(09 海南卷)2.一根容易形变的弹性导线,两端固定。导线中通有电流,方向如图中箭头所示。当没有磁场时,导线呈直线状态:当分别加上方向竖直向上、水平向右或垂直于纸面向外的匀强磁场时,描述导线状态的四个图示中正确的是D
海南卷)2.一根容易形变的弹性导线,两端固定。导线中通有电流,方向如图中箭头所示。当没有磁场时,导线呈直线状态:当分别加上方向竖直向上、水平向右或垂直于纸面向外的匀强磁场时,描述导线状态的四个图示中正确的是D
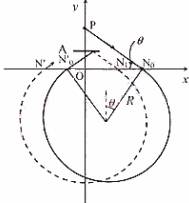
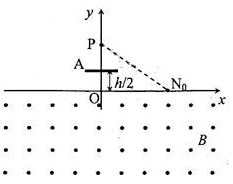 (09全国Ⅰ卷)26(21分) 如图,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于x y平面向外。P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点。A是一块平行于x轴的挡板,与x轴的距离为
(09全国Ⅰ卷)26(21分) 如图,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于x y平面向外。P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点。A是一块平行于x轴的挡板,与x轴的距离为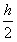 ,A的中点在y轴上,长度略小于
,A的中点在y轴上,长度略小于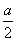 。带点粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度方向、大小不变。质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点。不计重力。求粒子入射速度的所有可能值。
。带点粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度方向、大小不变。质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点。不计重力。求粒子入射速度的所有可能值。
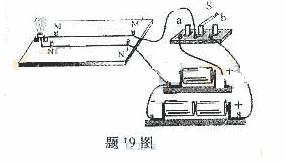
19.(09重庆卷)在题19图所示电路中,电池均相同,当电键S分别置于a、b两处时,导线 与
与 ,之间的安培力的大小为
,之间的安培力的大小为 、
、 ,判断这两段导线
,判断这两段导线
 A.相互吸引,
A.相互吸引, >
>
B.相互排斥, >
> 
C.相互吸引, <
<
D.相互排斥, <
<
答案:D
解析:电键S分别置于a、b两处时,电源分别为一节干电池、两节干电池,而电路中灯泡电阻不变,则电路中电流Ia<Ib, 在
在 处的磁感应强度Ba<Bb,应用安培力公式F=BIL可知
处的磁感应强度Ba<Bb,应用安培力公式F=BIL可知 <
< ,又
,又 在
在 电流方向相反、则相互排斥。
电流方向相反、则相互排斥。
(09广东理基卷) 13.电离子垂直匀强磁场方向运动时,会受到洛仑兹力的作用。下列表述正确的是
13.电离子垂直匀强磁场方向运动时,会受到洛仑兹力的作用。下列表述正确的是
 A.洛仑兹力对带电粒子做功
A.洛仑兹力对带电粒子做功 B.洛仑兹力不改变带电粒子的功能
B.洛仑兹力不改变带电粒子的功能
 C.洛仑兹力的大小与速度无关
C.洛仑兹力的大小与速度无关 D.洛仑兹力不改变带电粒兹的速度方向
D.洛仑兹力不改变带电粒兹的速度方向
 答案.B
答案.B
 [解析]根据洛伦兹力的特点,
洛伦兹力对带电粒子不做功,A错.B对.根据
[解析]根据洛伦兹力的特点,
洛伦兹力对带电粒子不做功,A错.B对.根据 ,可知大小与速度有关. 洛伦兹力的效果就是改变物体的运动方向,不改变速度的大小.
,可知大小与速度有关. 洛伦兹力的效果就是改变物体的运动方向,不改变速度的大小.
(09广东物理卷)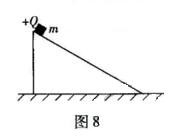 11.如图8所示,表面粗糙的斜面固定于地面上,并处于方向垂直纸面向外、强度为B的匀强磁场中。质量为m、带电量为+Q的小滑块从斜面顶端由静止下滑。在滑块下滑的过程中,下列判断正确的是
11.如图8所示,表面粗糙的斜面固定于地面上,并处于方向垂直纸面向外、强度为B的匀强磁场中。质量为m、带电量为+Q的小滑块从斜面顶端由静止下滑。在滑块下滑的过程中,下列判断正确的是
A.滑块受到的摩擦力不变
B.滑块到地面时的动能与B的大小无关
C.滑块受到的洛伦兹力方向垂直斜面向下
D.B很大时,滑块可能静止于斜面上
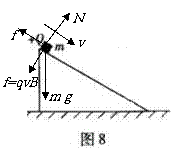 [答案]CD。
[答案]CD。
[解析]取物块为研究对象,小滑块沿斜面下滑由于受到洛伦兹力作用,如图所示,C正确;N=mgcosθ+qvB,由于v不断增大,则N不断增大,滑动摩擦力f=μN,摩擦力增大,A错误;滑块的摩擦力与B有关,摩擦力做功与B有关,依据动能定理,在滑块下滑到地面的过程中,满足 ,所以滑块到地面时的动能与B有关,B错误;当B很大,则摩擦力有可能很大,所以滑块可能静止在斜面上,D正确。
,所以滑块到地面时的动能与B有关,B错误;当B很大,则摩擦力有可能很大,所以滑块可能静止在斜面上,D正确。
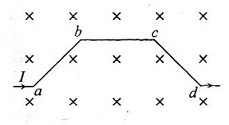
17.(09全国Ⅰ卷)如图,一段导线abcd位于磁感应强度大小为B的匀强磁场中,且与磁场方向(垂直于纸面向里)垂直。线段ab、bc和cd的长度均为L,且 。流经导线的电流为I,方向如图中箭头所示。流经导线段abcd所受到的磁场的作用力的合力
。流经导线的电流为I,方向如图中箭头所示。流经导线段abcd所受到的磁场的作用力的合力
A. 方向沿纸面向上,大小为
 B. 方向沿纸面向上,大小为
B. 方向沿纸面向上,大小为
C. 方向沿纸面向下,大小为
D. 方向沿纸面向下,大小为
答案A
[解析]本题考查安培力的大小与方向的判断.该导线可以用a和d之间的直导线长为 来等效代替,根据
来等效代替,根据 ,可知大小为
,可知大小为 ,方向根据左手定则.A正确.
,方向根据左手定则.A正确.
1.(09广东理基卷)发现通电导线周围存在磁场的科学家是
A.洛仑兹 B 库仑 C.法拉第 D奥斯特
答案.B
[解析]发现电流的磁效应的科学家是丹麦的奥斯特.而法拉第是发现了电磁感应现象
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com