1．(05年南京)如图所示，在用横截面为椭圆形的墨水瓶演示坚硬物体微小弹性形变的演示实验中，能观察到的现象是( B )　 　　　　 　　

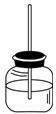A．沿椭圆长轴方向压瓶壁，管中水面上升；

沿椭圆短轴方向压瓶壁，管中水面下降

B．沿椭圆长轴方向压瓶壁，管中水面下降；

沿椭圆短轴方向压瓶壁，管中水面上升

C．沿椭圆长轴或短轴方向压瓶壁，管中水面均上升　

D．沿椭圆长轴或短轴方向压瓶壁，管中水面均下降

4．分析平衡问题的基本方法：

①合成法或分解法：当物体只受三力作用处于平衡时，此三力必共面共点，将其中的任意两个力合成，合力必定与第三个力大小相等方向相反；或将其中某一个力(一般为已知力)沿另外两个力的反方向进行分解，两分力的大小与另两个力大小相等．

②正交分解法：当物体受三个或多个力作用平衡时，一般用正交分解法进行计算．

规律方法

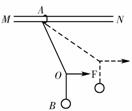
[例1](05年浦东)如图所示，轻绳的两端分别系在圆环A和小球B上，圆环A套在粗糙的水平直杆MN上?现用水平力F拉着绳子上的一点O，使小球B从图示实线位置缓慢上升到虚线位置，但圆环A始终保持在原位置不动则在这一过程中，环对杆的摩擦力F_f和环对杆的压力F_N的变化情况　　 　　　　　　　　　　　　　　　　　(　B　)

A．F_f不变，F_N不变　　　B．F_f增大，F_N不变　　　　　　

C．F_f增大，F_N减小　　　D．F_f不变，F_N减小

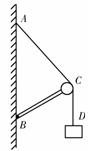训练题　如图所示，轻杆BC一端用铰链固定于墙上，另一端有一小滑轮C，重物系一绳经C固定在墙上的A点，滑轮与绳的质量及摩擦均不计?若将绳一端从A点沿墙稍向上移，系统再次平衡后，则　　　　　　　　　　　 　　(　C　)

A．轻杆与竖直墙壁的夹角减小

B．绳的拉力增大，轻杆受到的压力减小

C．绳的拉力不变，轻杆受的压力减小

D．绳的拉力不变，轻杆受的压力不变

[例2](05年高考)如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为m_A、m_B，弹簧的劲度系数为k，C为一固定挡板．系统处于静止状态．现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度a和从开始到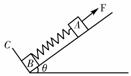此时物块A的位移d．(重力加速度为g)

[解]系统静止时，弹簧处于压缩状态，分析A物体受力可知：

F₁ = m_Agsinθ，F₁为此时弹簧弹力，设此时弹簧压缩量为x₁，则

F₁ = kx₁，得x₁ =

在恒力作用下，A向上加速运动，弹簧由压缩状态逐渐变为伸长状态．当B刚要离开C时，弹簧的伸长量设为x₂，分析B的受力有：

kx₂ = m_Bgsinθ，得x₂ =

设此时A的加速度为a，由牛顿第二定律有：

F-m_Agsinθ-kx₂ = m_Aa，得a =

A与弹簧是连在一起的，弹簧长度的改变量即A上移的位移，故有d = x₁+x_2，即：

d =

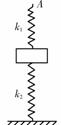训练题 　如图所示，劲度系数为k₂的轻质弹簧竖直放在桌面上，其上端压一质量为m的物块，另一劲度系数为k₁的轻质弹簧竖直地放在物块上面，其下端与物块上表面连接在一起要想使物块在静止时，下面簧产生的弹力为物体重力的，应将上面弹簧的上端A竖直向上提高多少距离？

答案：d = 5(k₁+k₂) mg/3k₁k₂

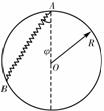[例3]如图所示，一个重为G的小球套在竖直放置的半径为R的光滑圆环上，一个劲度系数为k，自然长度为L(L＜2R)的轻质弹簧，一端与小球相连，另一端固定在大环的最高点，求小球处于静止状态时，弹簧与竖直方向的夹角φ．

[解析]小球受力如图所示，有竖直向下的重力G，弹簧的弹力F，　　　

圆环的弹力N，N沿半径方向背离圆心O．

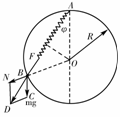利用合成法，将重力G和弹力N合成，合力F_合应与弹簧弹力F平衡观察发

现，图中力的三角形△BCD与△AOB相似，设AB长度为l由三角形相似有：

= 　= ，即得F =

另外由胡克定律有F = k(l-L)，而l = 2Rcosφ

联立上述各式可得：cosφ = ，φ = arcos?

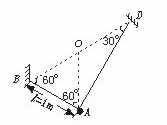
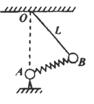训练题如图所示，A、B两球用劲度系数为k的轻弹簧相连，B球用长为L的细绳悬于0点，A球固定在0点正下方，且O、A间的距离恰为L，此时绳子所受的拉力为F₁，现把A、B间的弹簧换成劲度系数为k₂的轻弹簧，仍使系统平衡，此时绳子所受的拉力为F₂，则F₁与F₂大小之间的关系为　 (　 C　 )

　 A．F₁<F₂　 　　　　B． F₁>F₂　 　　　　C．F₁=F₂　 　　　　D．无法确定

[例4]如图有一半径为r = 0.2m的圆柱体绕竖直轴OO′以ω = 9rad/s的角

速度匀速转动．今用力F将质量为1kg的物体A压在圆柱侧面，使其以v₀ = 2.4m/s的速度匀速下降．若物体A与圆柱面的摩擦因数μ = 0.25，求力F的大小．(已知物体A在水平方向受光滑挡板的作用，不能随轴一起转动．)

[解析]在水平方向圆柱体有垂直纸面向里的速度，A相对圆柱体有纸垂直纸面向外的速度为υ′，υ′ = ωr = 1.8m/s；在竖直方向有向下的速度υ₀ = 2.4m/s

A相对于圆柱体的合速度为υ= = 3m/s

合速度与竖直方向的夹角为θ，则cosθ = =

A做匀速运动，竖直方向平衡，有F_f cosθ = mg，得F_f = = 12.5N

另F_f =μF_N，F_N =F，故F = 　= 50N

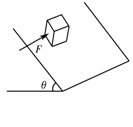
训练题 质量为m的物体，静止地放在倾角为θ的粗糙斜面上，现给物体一个大小为F的横向恒力，如图所示，物体仍处于静止状态，这时物体受的摩擦力大小是多少？

答案： f={F²+(mgsinθ)²}^1/2

能力训练

3．图解法：

图解法可以定性地分析物体受力的变化，适用于三力作用时物体的平衡．此时有一个力(如重力)大小和方向都恒定，另一个力方向不变，第三个力大小和方向都改变，用图解法即可判断两力大小变化的情况．

2．弹力和摩擦力：

平面接触面间产生的弹力，其方向垂直于接触面;曲面接触面间产生的弹力，其方向垂直于过接触点的曲面的切面；绳子产生的弹力的方向沿绳指向绳收缩的方向，且绳中弹力处处相等(轻绳)；杆中产生的弹力不一定沿杆方向，因为杆不仅可以产生沿杆方向的拉、压形变，也可以产生微小的弯曲形变．

分析摩擦力时，先应根据物体的状态分清其性质是静摩擦力还是滑动摩擦力，它们的方向都是与接触面相切，与物体相对运动或相对运动趋势方向相反．滑动摩擦力由F_f = μF_N公式计算，F_N为物体间相互挤压的弹力；静摩擦力等于使物体产生运动趋势的外力，由平衡方程或动力学方程进行计算．

1．动态平衡：

若物体在共点力作用下状态缓慢变化，其过程可近似认为是平衡过程，其中每一个状态均为平衡状态，这时都可用平衡来处理．

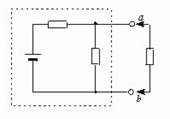
6.(★★★★★)如图26-11所示，虚线框内各元件的参数均不知。在a 、b端接一只R₁ = 10Ω的电阻时，测得其中I₁ = 1A ；若在a、b间换接电阻R₂ = 18Ω时，测得I₂ = 0.6A ；换接电阻R₃时，测得其中电流I₃ = 0.1A ，则R₃的阻值为多少？

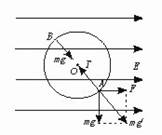
5.(★★★★)如图26-10所示，在竖直平面内有一场强E = 10⁴N/C的水平匀强电场，一质量m = 0.04kg ，带电量为q = 3×10⁵C的小球，用长l = 0.4m的细绳拴住悬于电场中O点，当小球平衡时，问在平衡位置以多大的线速度释放小球，则能使之在电场中做竖直平面内的圆周运动？

4.(★★★)一双线摆如图26-9所示，当它在垂直于纸面方向做小角度的摆动时，则该双线摆的周期T =________。

图26-9	图26-10	图26-11

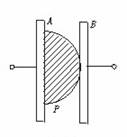
3.(★★★★)(图形变换的等效)一块均匀半圆薄片电阻合金片P ，先将它按图(26-7)方式接在A 、B之间，测得它的电阻为R ，然后按图(26-8)方式接在电极C 、D之间，这时P的电阻为________。

图26-6	图26-7	图26-8

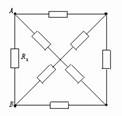
2.(★★★)(1999年上海)图26-6电路由8个不同的电阻组成，已知R₁ = 12Ω ，其余电阻阻值未知，测得A 、B间的总电阻为4Ω 。今将R₁换成6Ω的电阻，则A 、B间的总电阻为__________Ω 。(提示：用等效替代法)