
2.对于含有绝对值的不等式,如果其中含有字母参数,则根据基本的绝对值不等式的解法进行分类讨论,讨论时,不重复,也不要遗漏.
1.对含有绝对值的不等式的解法,通过上面的例子我们可以看到,其关键就在于去掉绝对值,而去掉绝对值,则需要对绝对值中的零点进行讨论,一般来说一个零点分两个范围,两个零点分三个零点,依次类推.
课本第16页练习1、2
例1 解不等式 1 | 2x-1 | < 5.
| 2x-1 | < 5.
分析:怎么转化?怎么去掉绝对值?
方法:原不等式等价于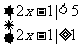

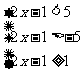 ① 或
① 或 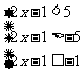 ②
②
解①得:1 x<3 ; 解②得:-2< x
x<3 ; 解②得:-2< x  0.
0.
∴原不等式的解集为 {x |
-2< x  0或1
0或1 x<3}
x<3}
方法2:原不等式等价于 1 2x-1<5或 –5<2x-1
2x-1<5或 –5<2x-1 -1
-1
即2 2x<6 或 –4<2x
2x<6 或 –4<2x 0.
0.
解得 1 x<3 或 –2< x
x<3 或 –2< x  0.
0.
∴原不等式的解集为{x |
-2< x  0或1
0或1 x<3}
x<3}
小结:比较两种解法,第二种解法比较简单,在解法二中,去掉绝对值符号的依据是 a | x |
| x | b
b a
a x
x b
b 或 -b
或 -b x
x -a (a
-a (a 0).
0).
练习:解下列不等式: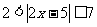
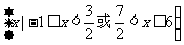
例2 解不等式:|4x-3|>2x+1.
分析:关键是去掉绝对值
方法1:原不等式等价于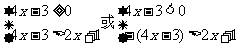 ,
,
即 , ∴x>2或x<
, ∴x>2或x< ,
,
∴原不等式的解集为{x| x>2或x< }.
}.
方法2:整体换元转化法
分析:把右边看成常数c,就同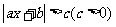 一样
一样
∵|4x-3|>2x+1 4x-3>2x+1或4x-3<-(2x+1)
4x-3>2x+1或4x-3<-(2x+1)  x>2 或x<
x>2 或x< ,
,
∴原不等式的解集为{x| x>2或x< }.
}.
例3 解不等式:|x-3|-|x+1|<1.
分析:关键是去掉绝对值
方法1:零点分段讨论法(利用绝对值的代数定义)
①当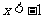 时,
时,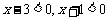
∴ ∴ 4<1
∴ 4<1 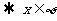
②当 时
时
∴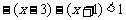

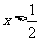 ,∴
,∴
③当 时
时
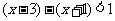
 -4<1
-4<1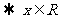 ∴
∴
综上 原不等式的解集为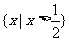
也可以这样写:
解:原不等式等价于① 或②
或②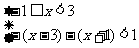 或 ③
或 ③ ,
,
解①的解集为φ,②的解集为{x| <x<3},③的解集为{x|x
<x<3},③的解集为{x|x 3},
3},
∴原不等式的解集为{x|x> }.
}.
方法2:数形结合
从形的方面考虑,不等式|x-3|-|x+1|<1表示数轴上到3和-1两点的距离之差小于1的点

∴原不等式的解集为{x|x> }.
}.
练习:解不等式:| x+2 | + | x | >4.
分析1:零点分段讨论法
解法1:①当x -2时,不等式化为 -(x+2)- x > 4 即x<-3. 符合题义
-2时,不等式化为 -(x+2)- x > 4 即x<-3. 符合题义
②当 –2<x<0时,不等式化为x+2-x>x即2>4.不合题义,舍去
③当x 0时,不等式化为x+2+x>4即x>1.符合题义
0时,不等式化为x+2+x>4即x>1.符合题义
综上:原不等式的解集为{x | x<-3或x>1}.
分析2:从形的方面考虑,不等式| x+2 | + | x | >4表示数轴上到-2和0两点的距离之和大于4的点
解法2:因取数轴上点1右边的点及点-3左边的点到点-2、0的距离之和均大于4
∴原不等式的解集为 {x | x<-3或 x>1}.
例4.解关于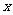 的不等式①
的不等式①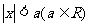 ,②
,②
解:∵ ,分类讨论如下
,分类讨论如下
① Ⅰ.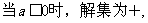
Ⅱ 
① Ⅰ.
Ⅱ 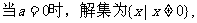
Ⅲ 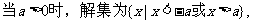
例5.解关于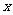 的不等式
的不等式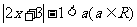 .
.
解:原不等式化为: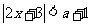 ,在求解时由于a+1的正负不确定,需分情况讨论.
,在求解时由于a+1的正负不确定,需分情况讨论.
①当a+1 0即a
0即a -1时,由于任何实数的绝对值非负,∴解集为
-1时,由于任何实数的绝对值非负,∴解集为 .
.
②当a+1>0即a> -1时,- (a+1)<2x+3< a+1 => 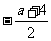 < x <
< x <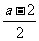 .
.
综上得: ①
②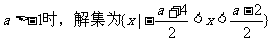 .
.
练习:课本第16页练习1、2
备用例题
例1.解下列不等式:(1)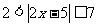 (2)
(2)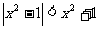
解(1)  (2)
(2) 
例2.已知不等式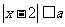
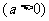 的解集为
的解集为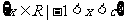 ,求
,求 的值.
的值. 
例3.解关于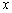 的不等式.
的不等式.


 .
.
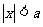 与
与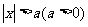 型不等式
型不等式 与
与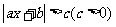 型不等式的解法与解集
型不等式的解法与解集
不等式 的解集是
的解集是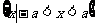 ;
;
不等式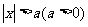 的解集是
的解集是
不等式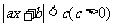 的解集为
的解集为  ;
;
不等式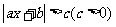 的解集为
的解集为 
29.(12分)某市政府坚持“忧民之所忧,乐民之所乐”的理念,构建社会主义和谐社会。在网上开展“市民论坛”活动,就如何“构建和谐社会”公开征集市民建议,问计于民。通过网上调查,发现本市在经济发展、社会进步的同时,面临这以下群众反映强烈的问题:
①房价上涨比较快,中低价位、中小户型房屋严重供不应求;
②居民收入差距过大,10%最高收入家庭的财产总额是10%最低收入家庭的30倍;
③刑事案件时有发生,社会秩序不稳定。
(1)运用《政治生活》知识说明该市政府问计于民做法的意义。(6分)
(2)假如你被选为该市“市民论坛”代表,请从政府职能的角度就该市所面临的问题向政府提出合理化建议。(6分)
26.(10分)有专家认为,2009年中国经济的增长得益于政府的刺激政策。虽然经济止跌回暖的趋势逐渐明朗化,但是仍要关注经济复苏中的挑战和风险,例如:社会公平问题、经济结构问题、贸易保护主义等风险因素,再次考验着中国经济的复苏前景。
结合材料回答:
“社会公平”是中国经济复苏中的挑战和风险之一,从经济生活角度谈谈怎样解决中国社会的公平问题?
25.2009年9月,上海白领张军(化名)因好心帮载自称胃痛要去医院的路人,结果却被城市交通执法大队认定为载客黑车,遭扣车与罚款1万元。原来那名路人是执法大队的“钩子”,专门诱人入瓮的。城市交通执法大队的这一做法遭到群众的普遍谴责。这一事例对人们的启示是 ( )
A.政府要尊重公民的基本政治权利
B.有些事情政府办不了,也不应该办
C.中国共产党要依法执政,要树立党的权威
D.政府要合法行政、合理行政
第Ⅱ卷(共计50分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com