
3.空间向量的直角坐标运算律:(1)若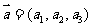 ,
,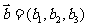 ,
,
则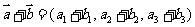 ,
,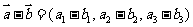 ,
,
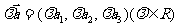 ,
,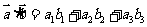 ,
,
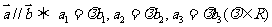 ,
,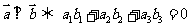 .
.
(2)若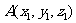 ,
,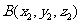 ,则
,则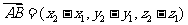 .
.
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标
4模长公式:若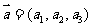 ,
则
,
则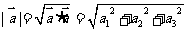 .
.
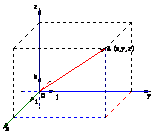 1空间直角坐标系:(1)若空间的一个基底的三个基向量互相垂直,且长为
1空间直角坐标系:(1)若空间的一个基底的三个基向量互相垂直,且长为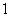 ,这个基底叫单位正交基底,用
,这个基底叫单位正交基底,用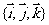 表示;(2)在空间选定一点
表示;(2)在空间选定一点 和一个单位正交基底
和一个单位正交基底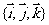 ,以点
,以点 为原点,分别以
为原点,分别以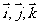 的方向为正方向建立三条数轴:
的方向为正方向建立三条数轴: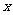 轴、
轴、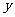 轴、
轴、 轴,它们都叫坐标轴.我们称建立了一个空间直角坐标系
轴,它们都叫坐标轴.我们称建立了一个空间直角坐标系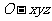 ,点
,点 叫原点,向量
叫原点,向量
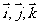 都叫坐标向量.通过每两个坐标轴的平面叫坐标平面,分别称为
都叫坐标向量.通过每两个坐标轴的平面叫坐标平面,分别称为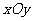 平面,
平面, 平面,
平面,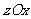 平面;
平面;
2.空间直角坐标系中的坐标: 在空间直角坐标系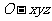 中,对空间任一点
中,对空间任一点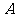 ,存在唯一的有序实数组
,存在唯一的有序实数组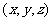 ,使
,使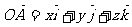 ,有序实数组
,有序实数组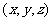 叫作向量
叫作向量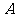 在空间直角坐标系
在空间直角坐标系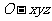 中的坐标,记作
中的坐标,记作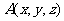 ,
,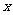 叫横坐标,
叫横坐标,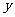 叫纵坐标,
叫纵坐标, 叫竖坐标.
叫竖坐标.
5.在△ABC中,已知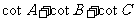 =
=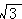 ,判定△ABC是什么三角形。
,判定△ABC是什么三角形。
※§8.3空间向量及其运算
4.在△ABC中,已知B=30°,b=50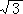 ,c=150,解三角形并判断三角形的形状。
,c=150,解三角形并判断三角形的形状。
3.某人在C点测得塔顶A在南偏西80°,仰角为45°,此人沿南偏东40°方向前进10米到0,测得塔顶A仰角为30°,则塔高= 。
2.△ABC中,若边a:b:c=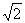 :(1+
:(1+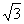 ):2,则内角A=
。
):2,则内角A=
。
1.已知锐角三角形的边长分别为2,3,x,则第三边x的取值范围是( )
A.1<x<5 B.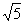 <x<
<x<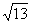 C.
C.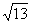 <x<5 D.1<x<
<x<5 D.1<x<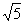
2.由于本节内容与代数、几何联系比较紧,故读者需对解斜三角形、解析几何中的圆锥曲线等知识非常熟悉方可。
三 经典例题导讲
[例1]在ABC中,已知a2=b2+bc+c2,则角A为( )
A.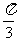 B.
B.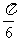 C.
C.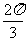 D.
D.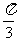 或
或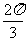
错解:选A
错因:公式记不牢,误将余弦定理中的“减”记作“加”。
正解:∵a2=b2+bc+c2=b2+c2-2bc(-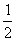 )=b2+c2-2bc·cos
)=b2+c2-2bc·cos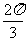
∴∠A=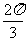
选 C.
[例2]在△ABC中,已知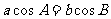 ,试判别其形状。
,试判别其形状。
错解:等腰三角形。
错因:忽视了两角互补,正弦值也相等的情形。直接由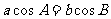 得,
得,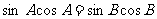 ,即
,即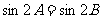 ,则
,则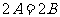 。接着下结论,所求三角形为等腰三角形
。接着下结论,所求三角形为等腰三角形
正解:由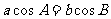 得,
得,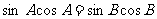 ,即
,即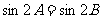
则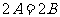 或
或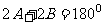 ,故三角形为直角三角形或等腰三角形。
,故三角形为直角三角形或等腰三角形。
[例3]过抛物线:y2=2px(p>0)顶点O作两条互相垂直的弦OA、OB(如图),求证:直线AB过一定点,并求出这一定点.
分析: 对于向量a=(x1,y1),b=(x2,y2),有a//b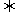 x1y2-x2y1=0.可以用来处理解析几何中的三点共线与两直线平行问题.
x1y2-x2y1=0.可以用来处理解析几何中的三点共线与两直线平行问题.
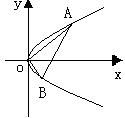 证明:由题意知可设A点坐标为(
证明:由题意知可设A点坐标为(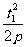 ,t1),B点坐标为(
,t1),B点坐标为(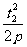 ,t2)
,t2)
∴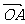 =(
=(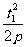 ,t1),
,t1), 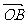 =(
=(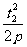 ,t2),
,t2),
∵OA⊥OB,∴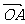 •
•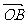 =0
=0
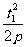 •
•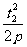 +t1•t2=0
+t1•t2=0
 t1•t2=-4p2 ①
t1•t2=-4p2 ①
设直线AB过点M(a,b),则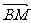 =(a-
=(a-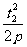 ,b-t2),
,b-t2),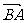 =(
=(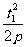 -
-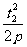 ,t1-t2),
,t1-t2),
由于向量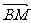 与
与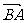 是共线向量,∴(a-
是共线向量,∴(a-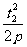 )(t1-t2)= (b-t2)(
)(t1-t2)= (b-t2)(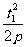 -
-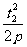 )
)
化简得2p(a-2p)=b(t1+t2)
显然当a=2p,b=0时等式对任意的成立
∴直线AB过定点,且定点坐标为M(2p,0)
四 典型习题导练
1.初中学过的勾股定理只是余弦定理的一种特殊情况。如当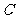 =
=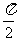 时,
时, =0,此时有
=0,此时有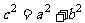 ;
;
2.正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即
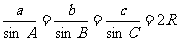
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com