
18.(12分) 设函数 .
.
(1)解不等式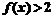 ;
;
(2)求函数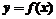 的最小值.
的最小值.
17.(10分)设p:实数x满足x2-4ax+3a2<0,其中a<0;q:实数x满足x2-x-6≤0,或x2+2x-8>0,且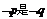 的必要不充分条件,求a的取值范围.
的必要不充分条件,求a的取值范围.
16、 给出下列四个命题:
①若a>b>0,c>d>0,那么 ;②已知a、b、m都是正数,并且a<b,则
;②已知a、b、m都是正数,并且a<b,则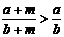 ;
;
③若a、b∈R,则a2+b2+5≥2(2a-b);④函数f(x)=2-3x- 的最大值是2-4
的最大值是2-4 .
.
⑤原点与点(2,1)在直线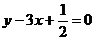 的异侧.
的异侧.
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
15.已知函数f (x) = 3ax-2a + 1在区间 (-1,1)内存在x0;使f (x0) = 0,则实数a的取值范围是 .
14.已知函数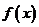 是偶函数,并且对于定义域内任意的
是偶函数,并且对于定义域内任意的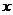 ,满足
,满足 ,
,
若当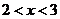 时,
时,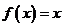 ,则
,则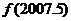 =__________
______.
=__________
______.
13. 函数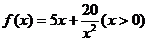 的最小值为_____________.
的最小值为_____________.
11.若f (x)是偶函数,且当x∈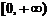 时,f (x) = x-1,则f (x-1) < 0的解集是( )
时,f (x) = x-1,则f (x-1) < 0的解集是( )
A.{x |-1 < x < 0} B.{x | x < 0或1< x < 2}
C.{x | 0 < x < 2} D.{x | 1 < x < 2}
12设函数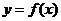 存在反函数
存在反函数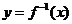 ,且函数
,且函数 的图象过点(1,2),则函数
的图象过点(1,2),则函数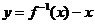 的图象一定过点(
)
的图象一定过点(
)
A.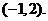 B.(2,1) C.(2,3)
D.(1,1)
B.(2,1) C.(2,3)
D.(1,1)
10.函数 的定义域为R,若
的定义域为R,若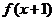 与
与 都是奇函数,则( )
都是奇函数,则( )
A. 是偶函数
B.
是偶函数
B. 是奇函数
是奇函数
C.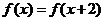 D.
D. 是奇函数
是奇函数
9.定义在R上的函数f(x)满足f(x)= 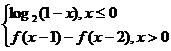 ,
,
则f(2009)的值为 ( )
A.-1 B. 0 C.1 D. 2
8.已知函数f (x) = 3-2 |x|, g(x) = x2-2x,构造函数y = F(x),定义如下:当f (x)≥g (x)时,F(x) = g(x);当f (x) < g (x)时,F(x) = f (x),那么F(x) ( )
A.有最大值3,最小值-1 B.有最大值3,无最小值
C.有最大值7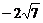 ,无最小值 D.无最大值,也无最小值
,无最小值 D.无最大值,也无最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com