2、下列词语中加点字的读音全部不相同的一组是(　 　　)

A．癖好　 辟谣　 　雷劈　 劈头盖脸　　 取譬设喻

B．作祟　 茁壮　 拙劣　 相形见绌 　　咄咄逼人

C．悱恻　 翡翠　 菲薄 　流言蜚语　　 斐然可观

D．泥淖　 悼念　 婥约　 踔厉风发　　 绰绰有余

1、下列词语中加点的字，每对的读音完全相同的一组是(　　 )

A．落笔／落寞　　 剥削／瘦削不堪 　　靡靡之音／风靡一时

B．刹那／古刹　　 　累赘／果实累累 　　强弩之末／强词夺理

C．佣工／佣金　　 攒射／万头攒动　　 解甲归田／解囊相助

D．殷红／殷切　　 　绰约／绰绰有余　　 擢发难数／数典忘祖

12．(16分)在△ABC中，角A，B，C所对的边分别为a，b，c.已知m＝，n＝，且满足|m+n|＝.

(1)求角A的大小；

(2)若|A|+|A|＝|B|，试判断△ABC的形状．

[解析]　(1)由|m+n|＝，得m²+n²+2m·n＝3，

即1+1+2＝3，

∴cos A＝，∵0＜A＜π，∴A＝.

(2)∵|A|+|A|＝|B|，∴b+c＝a，

∴sin B+sin C＝sin A，

∴sin B+sin＝×，即sin B+cos B＝，

∴sin＝.∵0＜B＜，∴＜B+＜，

∴B+＝或，故B＝或.当B＝时，C＝；当B＝时，C＝.故△ABC是直角三角形．

11．(15分)如图，＝，＝，＝.

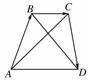
(1)若∥，求x与y间的关系；

(2)若有⊥，求x，y的值及四边形ABCD的面积．

[解析]　(1)+＝＝(x－2，y－3)，

+＝＝(x+4，y－2)，

若∥，则存在实数λ，有(x，y)＝λ(x+4，y－2)，

即消去λ，得x+2y＝0.①

(2)＝+＝(6+x,1+y)，

若⊥，有(6+x,1+y)·(x－2，y－3)＝0，x²+y²+4x－2y－15＝0.②

由①②，解得或

当时，＝(0,4)，||＝4；

＝(－8,0)，||＝8，

∵⊥，∴四边形ABCD面积S＝×4×8＝16.

当时，＝(8,0)，||＝8，＝(0，－4)，

||＝4，∴S＝16.

故或四边形ABCD的面积是16.

10．(15分)已知|a|＝1，|b|＝，a与b的夹角为θ.

(1)若a∥b，求a·b；

(2)若a－b与a垂直，求θ.

[解析]　(1)∵a∥b，∴θ＝0或π，

∴a·b＝|a||b|cos θ＝1××cos　 θ＝±.

(2)∵(a－b)⊥a，∴a·(a－b)＝0，

即a²－a·b＝0，∴1－1×cos θ＝0，∴cos　 θ＝.

∵θ∈[0，π]，∴θ＝.

9．(2009年天津卷)若等边△ABC的边长为2，平面内一点M满足＝+，则·＝________.

[解析]　如图所示．

·＝(－)·(－)

＝·

＝·

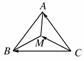
＝·－²－²+·

＝·－²－²

＝×(2)²×－(2)²－(2)²

＝－2.

[答案]　－2

8．(2008年陕西卷)关于平面向量a，b，c，有下列三个命题：

①若a·b＝a·c，则b＝c.

②若a＝(1，k)，b＝(－2,6)，a∥b，则k＝－3.

③非零向量a和b满足|a|＝|b|＝|a－b|，则a与a+b的夹角为60°.

其中真命题的序号为________(写出所有真命题的序号)．

[解析]　命题①明显错误．由两向量平行的充要条件得1×6+2k＝0，k＝－3，故命题②正确．由|a|＝|b|＝|a－b|，

再结合平行四边形法则可得a与a+b的夹角为30°，命题③错误．

[答案]　②

7．在长江南岸渡口处，江水以12.5 km/h的速度向东流，渡船的速度为25 km/h.渡船要垂直地渡过长江，则航向为________．

[解析]　如图，渡船速度为，水流速度为，船实际垂直过江的速度为，依题意知，|O|＝12.5，|O|＝25，由于四边形OADB为平行四边形，则|B|＝|O|，又OD⊥BD，

∴在Rt△OBD中，∠BOD＝30°，∴航向为北偏西30°.

[答案]　北偏西30°

6．已知非零向量，和满足·＝0，且＝，则△ABC为

(　)

A．等边三角形　 　　　　　　　　　　　 B．等腰非直角三角形

C．非等腰三角形　 　　　　　　　　　 D．等腰直角三角形

[解析]　由于+表示的向量所在直线，是∠BAC的平分线，故·＝0说明∠BAC的平分线与BC垂直，故说明三角形ABC为等腰三角形，

又＝cos∠ACB＝⇒∠ACB＝，故三角形为等腰直角三角形．

[答案]　D

5．已知||＝1，||＝，·＝0，点C在∠AOB内，且∠AOC＝30°.设＝m+nOB(m，n∈R)，则等于

(　)

A.　 　　　　　　　　　　　　　　　　　　　　 B．3

C.　 　　　　　　　　　　　　　　　　　　　 D.

[解析]　解法1：　如图建立直角坐标系：

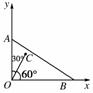
＝m(0,1)+n(，0)＝(n，m)

∴＝tg60°＝，∴＝3.

解法2：　∵cos∠COB＝cos∠60°，

∴＝，

∴＝⇒＝⇒＝，

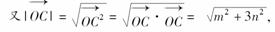
∴＝⇒＝9，∴＝3.

[答案]　B