
2. 已知随机变量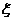 服从正态分布
服从正态分布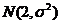 ,
,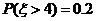 ,则
,则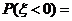 (
)
(
)
A. 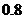 B.
B.
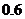 C.
C.
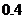 D.
D.
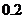
1.在复平面内,复数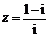 (
(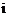 是虚数单位)对应的点位于
(
)
是虚数单位)对应的点位于
(
)
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6.已知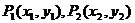 ,当
,当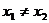 时,直线
时,直线 的斜率
的斜率 =
;当
=
;当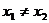 且
且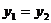 时,直线
时,直线 的斜率为
,倾斜角为 .
的斜率为
,倾斜角为 .
5.已知O(0,0)、P(a,b)(a≠0),直线OP的斜率是 .
4.已知M(a,b)、N(a,c)(b≠c),则直线MN的倾斜角是 .
3.已知A(2,3)、B(-1,4),则直线AB的斜率是 .
2.过点P(-2,m)和Q(m,4)的直线的斜率等于1,则m的值为( )
A.1 B.4 C.1或3 D.1或4
1.直线 经过原点和点(-1,-1),则它的倾斜角是( )
经过原点和点(-1,-1),则它的倾斜角是( )
A.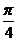 B.
B. 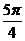 C.
C.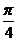 或
或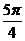 D.-
D.-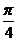
例1 如图,直线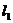 的倾斜角
的倾斜角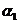 =30°,直线
=30°,直线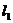 ⊥
⊥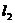 ,求
,求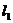 、
、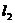 的斜率.
的斜率.
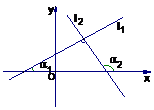 分析:对于直线
分析:对于直线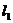 的斜率,可通过计算
的斜率,可通过计算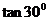 直接获得,而直线
直接获得,而直线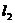 的斜率则需要先求出倾斜角
的斜率则需要先求出倾斜角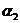 ,而根据平面几何知识,
,而根据平面几何知识, 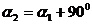 ,然后再求
,然后再求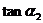 即可.
即可.
解: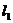 的斜率
的斜率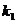 =tan
=tan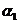 =tan30°=
=tan30°= ,
,
∵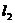 的倾斜角
的倾斜角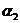 =90°+30°=120°,
=90°+30°=120°,
∴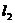 的斜率
的斜率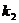 =tan120°=tan(180°-60°)=-tan60°=
=tan120°=tan(180°-60°)=-tan60°=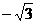 .
.
评述:此题要求学生掌握已知直线的倾斜角求斜率,其中涉及到三角函数的诱导公式及特殊角正切值的确定.
例2 已知直线的倾斜角,求直线的斜率:
(1)  =0°;(2)
=0°;(2) =60°;(3)
=60°;(3)  =90°;(4)
=90°;(4) =
=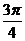
分析:通过此题训练,意在使学生熟悉特殊角的斜率.
解:(1)∵tan0°=0 ∴倾斜角为0°的直线斜率为0;
(2)∵tan60°=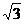 ∴倾斜角为60°的直线斜率为
∴倾斜角为60°的直线斜率为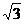 ;
;
(3)∵tan90°不存在 ∴倾斜角为90°的直线斜率不存在;
(4)∵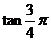 =
=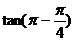 =-tan
=-tan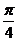 =-1,
=-1,
∴倾斜角为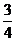 π的直线斜率为-1.
π的直线斜率为-1.
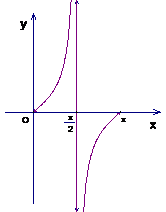
4.已知直线的倾斜角的取值范围,利用正切函数的性质,讨论直线斜率及其绝对值的变化情况:
(1)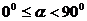
作出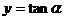 在
在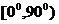 区间内的函数图象;由图象观察可知:当
区间内的函数图象;由图象观察可知:当 ∈
∈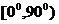 ,
,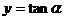 >0,并且随着
>0,并且随着 的增大,
的增大, 不断增大,
不断增大, 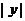 也不断增大.
也不断增大.
 所以,当
所以,当 ∈
∈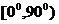 时,随着倾斜角
时,随着倾斜角 的不断增大,直线斜率不断增大,直线斜率的绝对值也不断增大.
的不断增大,直线斜率不断增大,直线斜率的绝对值也不断增大.
(2) 
作出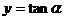 在
在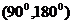 区间内的函数图象,由图象观察可知:当
区间内的函数图象,由图象观察可知:当 ∈
∈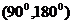 ,
,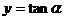 <0,并且随着
<0,并且随着 的增大,
的增大,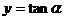 不断增大,
不断增大,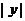 不断减小.
不断减小.
所以当 ∈
∈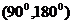 时,随着倾斜角
时,随着倾斜角 的不断增大,直线的斜率不断增大,但直线斜率的绝对值不断减小.
的不断增大,直线的斜率不断增大,但直线斜率的绝对值不断减小.
针对以上结论,虽然有当 ∈
∈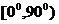 ,随着
,随着 增大直线斜率不断增大;当
增大直线斜率不断增大;当 ∈
∈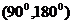 ,随着
,随着 增大直线斜率不断增大. 但是当
增大直线斜率不断增大. 但是当 ∈
∈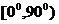 ∪
∪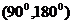 时,随着
时,随着 的增大直线斜率不断增大却是一错误结论. 原因在于正切函数
的增大直线斜率不断增大却是一错误结论. 原因在于正切函数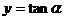 在区间
在区间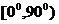 内为单调增函数,在区间
内为单调增函数,在区间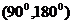 内也是单调增函数,但在
内也是单调增函数,但在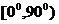 ∪
∪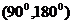 区间内,却不具有单调性
区间内,却不具有单调性
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com