
28.刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再往A镇参加救灾。一分队了发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时。
⑴若二分队在营地不休息,问二分队几小时能赶到A镇?
⑵若二分队和一分队同时赶到A镇,二分队应在营地休息几小时?
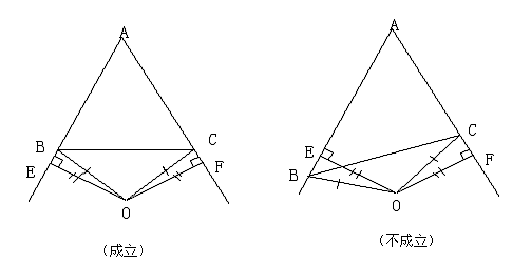
⑶下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义。

[命题意图]培养学生观察图形的能力和方法。
[参考答案](1)若二分队在营地不休息,则a=0,速度为4千米/时,行至塌方处需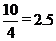 (小时)因为一分队到塌方处并打通道路需要
(小时)因为一分队到塌方处并打通道路需要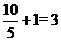 (小时),故二分队在塌方处需停留0.5小时,所以二分队在营地不休息赶到A镇需2.5+0.5+
(小时),故二分队在塌方处需停留0.5小时,所以二分队在营地不休息赶到A镇需2.5+0.5+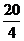 =8(小时) (2)一分队赶到A镇共需
=8(小时) (2)一分队赶到A镇共需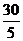 +1=7(小时)
+1=7(小时)
(Ⅰ)若二分队在塌方处需停留,则后20千米需与一分队同行,故4+a=5,即a=1,这与二分队在塌方处停留矛盾,舍去; (Ⅱ)若二分队在塌方处不停留,则(4+a)(7-a)=30,即a2-3a+2=0,,解得a1=1,a2=2均符合题意。答:二分队应在营地休息1小时或2小时。(其他解法只要合理即给分) 图像(b)表明二分队在营地休息时间过长(2<a≤3),后于一分队赶到A镇;
图像(d)表明二分队在营地休息时间恰当(1<a≤2),先于一分队赶到A镇。 ……14分
[试题来源]中考指南全真模拟试题
27.(本题满分14分)
“5·12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1) 请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
|
|
C |
D |
总计 |
|
A |
|
|
200吨 |
|
B |
x吨 |
|
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
(2) 设A、B两个蔬菜基地的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案;
(3) 经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少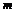 元(
元(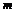 >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.
[命题意图]考查学生列方程解应用题。
[参考答案] (1)填表
|
|
C |
D |
总计 |
|
A |
(240-x)吨 |
(x-40)吨 |
200吨 |
|
B |
x吨 |
(300-x)吨 |
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
依题意得: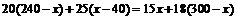 . ------------------------------4分
. ------------------------------4分
解得: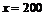 .
-----------------------------------------------------------------5分
.
-----------------------------------------------------------------5分
(2) w与x之间的函数关系为: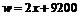 .
-------------------------------------8分
.
-------------------------------------8分
依题意得: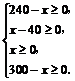 .
∴40≤
.
∴40≤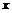 ≤240
----------------------------------9分
≤240
----------------------------------9分
在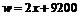 中,∵2>0, ∴
中,∵2>0, ∴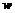 随
随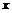 的增大而增大, 表一:
的增大而增大, 表一:
|
|
C |
D |
|
A |
200吨 |
0吨 |
|
B |
40吨 |
260吨 |
故当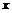 =40时,总运费最小, ---------------------10分
=40时,总运费最小, ---------------------10分
此时调运方案为如右表一. ----------------------11分
(3)由题意知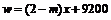
∴0<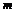 <2时,(2)中调运方案总运费最小;-----12分
<2时,(2)中调运方案总运费最小;-----12分
|
|
C |
D |
|
A |
0吨 |
200吨 |
|
B |
240吨 |
60吨 |
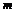 =2时,在40≤
=2时,在40≤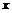 ≤240的前提下调运
表二:
≤240的前提下调运
表二:
方案的总运费不变; ------13分
2<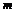 <15时,
<15时,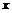 =240总运费最小,
=240总运费最小,
其调运方案如右表
[试题来源]初三月考试题改编
26. 杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分,如图。
的一部分,如图。
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由。
.[命题意图]抛物线和二次函数性质
[参考答案]1) =
=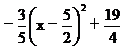 ……4分
……4分
∵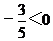 ,∴函数的最大值是
,∴函数的最大值是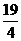 。
。
答:演员弹跳的最大高度是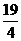 米。……6分
米。……6分
(2)当x=4时,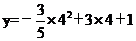 =3.4=BC,所以这次表演成功。……10分
=3.4=BC,所以这次表演成功。……10分
[试题来源]本校月考加工总结所得
25.甲同学口袋中有三张卡片,分别写着数字1、1、2,乙同学口袋中也有三张卡片,分别写着数字1、2、2。两人各自从自己的口袋中随机摸出一张卡片,若两人摸出的卡片上的数字之和为偶数,则甲胜;否则乙胜。求甲胜的概率
[命题意图]让学生掌握简单有理数的方法。
[参考答案]:所有可能的结果列表如下:
 |
|
|
|
|
1 |
偶数 |
偶数 |
奇数 |
|
2 |
奇数 |
奇数 |
偶数 |
|
2 |
奇数 |
奇数 |
偶数 |
………4分
由表可知,和为偶数的结果有4种,∴P(甲胜)=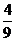 ,答:甲胜的概率是
,答:甲胜的概率是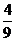 .……
.……
[试题来源]初三中考全真模拟试题
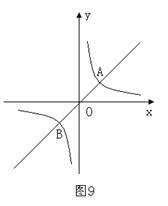
24.如图9,已知正比例函数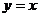 与反比例函数
与反比例函数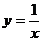 的图象交于
的图象交于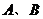 两点.
两点.
 (1)求出
(1)求出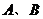 两点的坐标;
两点的坐标;
(2)根据图象求使正比例函数值大于反比例函数值的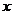 的范围;
的范围;
[命题意图]让学生正比例函数与反比例函数的运用
[参考答案](1)解方程组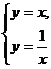 得,
得,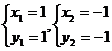 2分
2分
所以A、B两点的坐标分别为:A(1,1)、B(-1,-1) 4分
(2)根据图象知,当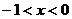 或
或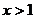 时,正比例函数值大于反比例函数值 8分
时,正比例函数值大于反比例函数值 8分
[试题来源]连云港中考全真模拟试题
23.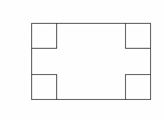 如图所示,在长和宽分别是
如图所示,在长和宽分别是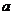 、
、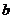 的矩形纸片的四个角都剪去一个边长为
的矩形纸片的四个角都剪去一个边长为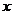 的正方形.
的正方形.
(1) 用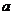 ,
,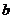 ,
,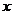 表示纸片剩余部分的面积;
表示纸片剩余部分的面积;
(2)
当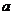 =6,
=6,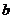 =4,且剪去部分的面积等于剩余部分的
=4,且剪去部分的面积等于剩余部分的
面积时,求正方形的边长.
[命题意图]让学生掌握正方形剩余部分的面积的方法。
[参考答案]如图所示,在长和宽分别是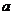 、
、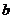 的矩形纸片的四个角都剪去一个边长为
的矩形纸片的四个角都剪去一个边长为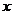 的正方形.
的正方形.
(3)
用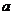 ,
,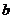 ,
,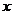 表示纸片剩余部分的面积;
表示纸片剩余部分的面积;
(4)
当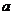 =6,
=6,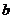 =4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.
=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.
 解:(1)
解:(1) 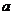
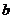 -4
-4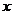 2;···································· 2分
2;···································· 2分
(2)依题意有: 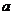
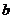 -4
-4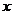 2=4
2=4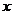 2,········ 4分
2,········ 4分
将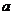 =6,
=6,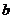 =4,代入上式,得
=4,代入上式,得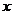 2=3, 6分
2=3, 6分
解得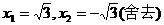 .··············· 8分
.··············· 8分
即正方形的边长为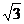 .
.
[试题来源]中考全真模拟试题
22.解不等式组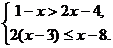
[命题意图]让学生掌握简单不等式组的解法
[参考答案]x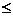 2
2
[试题来源]随堂练习改编
21.计算: 2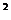 +
+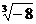 +2
+2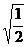 -(
-(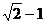 )
)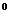
[命题意图]让学生掌握简单有理数的方法。
[参考答案]原式=4-2+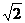 -1=1+
-1=1+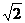
[试题来源]连云港中考全真模拟试题
20.一次函数y=-x+1与反比例函数y=-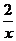 ,x与y的对应值如下表:
,x与y的对应值如下表:
|
x |
-3 |
-2 |
-1 |
1 |
2 |
3 |
|
y=-x+1 |
4 |
3 |
2 |
0 |
-1 |
-2 |
y=-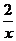 |
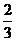 |
1 |
2 |
-2 |
-1 |
-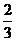 |
方程-x+1=-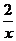 的解为___________;不等式-x+1>-
的解为___________;不等式-x+1>-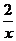 的解集为_________________.
的解集为_________________.
[命题意图]一次函数与反比例函数的性质运用
[参考答案]x1=-1,x2=2;x<-1或0<x<2;
[试题来源]连云港中考全真模拟试题
19.把函数y=-3x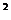 的图象沿x轴对折,得到的图象的解析式为_______.
的图象沿x轴对折,得到的图象的解析式为_______.
[命题意图]让学生掌握简单有理数的方法。
[参考答案]y=3x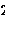
[试题来源]南京中考全真模拟试题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com