
5.18.[江苏·苏州](本小题满分15分)
经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t(件),价格近似满足 (元).
(元).
(Ⅰ)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(Ⅱ)求该种商品的日销售额y的最大值与最小值.
[解](Ⅰ)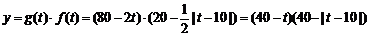 …… 4分
…… 4分
=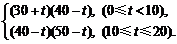 …………………… 8分
…………………… 8分
(Ⅱ)当0≤t<10时,y的取值范围是[1200,1225],
在t=5时,y取得最大值为1225; …………………… 11分
当10≤t≤20时,y的取值范围是[600,1200],
在t=20时,y取得最小值为600. …………………… 14分
(答)总之,第5天,日销售额y取得最大为1225元;
第20天,日销售额y取得最小为600元. …………………… 15分
4.[江苏·苏北四市]17.(本题满分14分) 某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价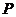 (元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
|
时间(将第x天记为x)x |
1 |
10 |
11 |
18 |
|
单价(元/件)P |
9 |
0 |
1 |
8 |
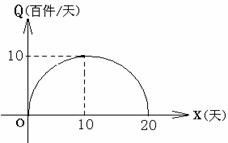 而这20天相应的销售量
而这20天相应的销售量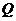 (百件/天)与
(百件/天)与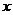 对应的点
对应的点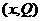 在如图所示的半圆上.
在如图所示的半圆上.
(Ⅰ)写出每天销售收入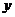 (元)与时间
(元)与时间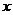 (天)的函数关系式
(天)的函数关系式 ;
;
(Ⅱ)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价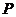 定为多少元为好?(结果精确到1元)
定为多少元为好?(结果精确到1元)
[解](1)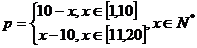 ,
………3分
,
………3分
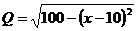 ,
,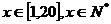 ,
………6分
,
………6分
∴ 。 ………8分
。 ………8分
(2)∵ ,……11分
,……11分
∴当且仅当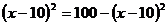 ,即
,即 时,
时,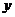 有最大值。……13分
有最大值。……13分
∵ ,∴取
,∴取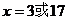 时,
时,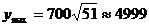 (元),
(元),
此时, (元)。答:第3天或第17天销售收入最高,此时应将单价
(元)。答:第3天或第17天销售收入最高,此时应将单价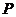 定为7元为好
定为7元为好
3.[江苏·启东中学模拟]19.(本小题满分16分)已知函数 (
( ).
).
(I)若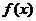 的定义域和值域均是
的定义域和值域均是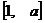 ,求实数
,求实数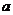 的值;
的值;
(II)若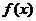 在区间
在区间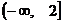 上是减函数,且对任意的
上是减函数,且对任意的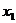 ,
,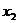
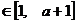 ,总有
,总有 ,求实数
,求实数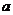 的取值范围.
的取值范围.
[解]∵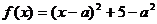 (
( ),
),
∴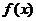 在
在 上是减函数,(2分)
上是减函数,(2分)
又定义域和值域均为 ,∴
,∴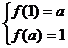 ,(4分)
,(4分)
即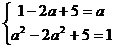 , 解得
, 解得 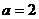 .(6分)
.(6分)
(II) ∵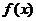 在区间
在区间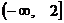 上是减函数,∴
上是减函数,∴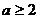 ,(8分)
,(8分)
又 ,且,
,且,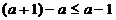
∴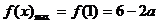 ,
, .(11分)
.(11分)
∵对任意的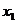 ,
,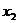
 ,总有
,总有 ,
,
∴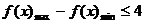 ,(13分)
,(13分)
即 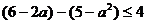 ,解得
,解得 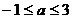 ,(14分)
,(14分)
又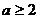 , ∴
, ∴ .(15分)
.(15分)
2.[江苏·启东中学模拟]18.(本小题满分16分)即将开工的上海与周边城市的城际列车铁路线将大大缓解交通的压力,加速城市之间的流通。根据测算,如果一列火车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次。每天来回次数是每次拖挂车厢个数的一次函数,每节车厢一次能载客110人,试问每次应拖挂多少节车厢才能使每天营运人数最多?并求出每天最多的营运人数。(注: 营运人数指火车运送的人数)
[解]设这列火车每天来回次数为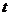 次,每次拖挂车厢
次,每次拖挂车厢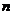 节
2分
节
2分
则设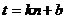 由
由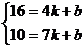 解得
解得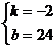
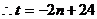 4分
4分
设每次拖挂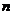 节车厢每天营运人数为
节车厢每天营运人数为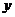 人
1分
人
1分
则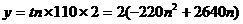 2分
2分
当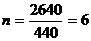 时,总人数最多为15840人
2分
时,总人数最多为15840人
2分
答:每次应拖挂6节车厢才能使每天的营运人数最多为15840人. 1分
1.[江苏·常州]19.(16分)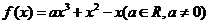 , (1)若
, (1)若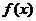 在
在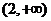 上单调递减,求
上单调递减,求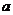 的取值范围; (2)证明:
的取值范围; (2)证明: 时,
时,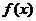 在
在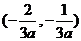 上不存在零点。
上不存在零点。
[解](1)方法一:分离参数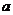 ,
, ,变成求函数的最小值
,变成求函数的最小值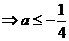 。
。
方法二:利用二次函数的知识解不等式。
(2)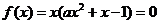
 的根不在
的根不在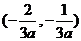 之间即可。
之间即可。
当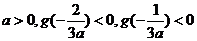 ,
,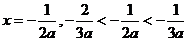
 的零点不在
的零点不在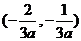 之间。
之间。
15.[江苏·泰州实验]4.已知一辆轿车在公路上作加速直线运动,设 时的速度为
时的速度为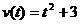
 ,则
,则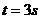 时轿车的瞬时加速度为_______6
时轿车的瞬时加速度为_______6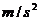 ________.
________.
14.[江苏·泰州实验]2.集合 ,若
,若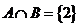 ,则
,则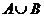 =
=
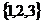 .
.
13.[江苏·泰州实验]1.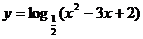 的定义域是_____
的定义域是_____ 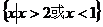 .
.
12.11.[江苏·苏州]已知函数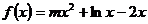 在定义域内是增函数,则实数
在定义域内是增函数,则实数 的取值范围为_____
的取值范围为_____ ____.
____.
11.4.[江苏·苏州]函数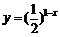 的值域是____(0,+∞)_____.
的值域是____(0,+∞)_____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com