练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知坐标原点O在圆x2+y2-x+y+m=0外，则m的取值范围是

    A．m>0
    B．m<
    C．0<m<
    D．m≤
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：0117 同步题 题型：单选题

    已知坐标原点O在圆x2+y2-x+y+m=0外，则m的取值范围是
    [     ]
    A．m>0
    B．m<
    C．0<m<
    D．m≤

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知⊙C：x2＋y2＋2x－4y＋1＝0.

    (1)若⊙C的切线在x轴、y轴上截距相等，求切线的方程．

    (2)从圆外一点P(x0，y0)向圆引切线PM，M为切点，O为原点，若|PM|＝|PO|，求使|PM|最小的P点坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知⊙C：x2＋y2＋2x－4y＋1＝0.

    (1)若⊙C的切线在x轴、y轴上截距相等，求切线的方程．

    (2)从圆外一点P(x0，y0)向圆引切线PM，M为切点，O为原点，若|PM|＝|PO|，求使|PM|最小的P点坐标．

    查看答案和解析>>

    科目：高中数学 来源：2015届广东省高一下学期第一次段考文科数学试卷（解析版） 题型：解答题

    已知⊙C：x2＋y2＋2x－4y＋1＝0.

    (1)若⊙C的切线在x轴、y轴上截距相等，求切线的方程．

    (2)从圆外一点P(x0，y0)向圆引切线PM，M为切点，O为原点，若|PM|＝|PO|，求使|PM|最小的P点坐标．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知⊙C：x2＋y2＋2x－4y＋1＝0.

    (1)若⊙C的切线在x轴、y轴上截距相等，求切线的方程．

    (2)从圆外一点P(x0，y0)向圆引切线PM，M为切点，O为原点，若|PM|＝|PO|，求使|PM|最小的P点坐标．

    查看答案和解析>>

    科目：高中数学 来源：江苏省无锡市洛社中学2012届高三上学期12月月考数学试题 题型：044

    已知圆C：x2＋y2＋2x－4y＋3＝0；

    (1)若圆C的切线在x轴，y轴上的截距相等，求此切线方程；

    (2)从圆C外一点P(x1，y1)向圆引一条切线，切点为M，O为原点，且有|PM|＝|PO|，求使|PM|最小的P点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

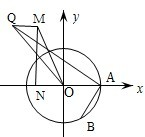    精英家教网已知以原点O为中心的椭圆的一条准线方程为y=
    4
    		3
    3
    ，离心率e=
    		3
    2
    ，M是椭圆上的动点
    （Ⅰ）若C，D的坐标分别是(0，-
    		3
    )，(0，
    		3
    )    ，求|MC|•|MD|的最大值；
    （Ⅱ）如题（20）图，点A的坐标为（1，0），B是圆x2+y2=1上的点，N是点M在x轴上的射影，点Q满足条件：
    OQ
    =
    OM
    +
    ON
    ，
    QA
    •
    BA
    =0    、求线段QB的中点P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

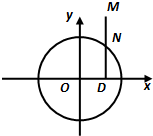    如图所示，点N在圆x2+y2=4上运动，DN⊥x轴，点M在DN的延长线上，且
    DM
    =λ
    DN
    （λ＞0）．
    （1）求点M的轨迹方程，并求当λ为何值时M的轨迹表示焦点在x轴上的椭圆；
    （2）当λ=
    1
    2
    时，（1）所得曲线记为C，已知直线l：
    x
    2
    +y=1    ，P是l上的动点，射线OP（O为坐标原点）交曲线C于点R，又点Q在OP上且满足|OQ|•|OP|=|OR|2，求点Q的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源：0119 期中题 题型：解答题

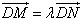    如图所示，点N在圆x2+y2=4上运动，DN⊥x轴，点M在DN的延长线上，且（λ＞0），
    （1）求点M的轨迹方程，并求当λ为何值时M的轨迹表示焦点在x轴上的椭圆；
    （2）当λ=时，（1）所得曲线记为C，已知直线l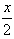：+y=1，P是l上的动点，射线OP（O为坐标原点）交曲线C于点R，又点Q在OP上且满足|OQ|·|OP|=|OR|2，求点Q的轨迹方程。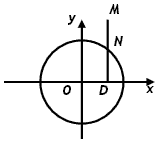

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，已知对于任意实数k，直线(
    		3
    k+1)x+(k-
    		3
    )y-(3k+
    		3
    )=0    恒过定点F．设椭圆C的中心在原点，一个焦点为F，且椭圆C上的点到F的最大距离为2+
    		3
    ．
    （1）求椭圆C的方程；
    （2）设（m，n）是椭圆C上的任意一点，圆O：x2+y2=r2（r＞0）与椭圆C有4个相异公共点，试分别判断圆O与直线l1：mx+ny=1和l2：mx+ny=4的位置关系．

    查看答案和解析>>


    同步练习册答案