
科目:高中数学 来源:2010-2011学年江苏省南京市高三第二次模拟考试数学卷 题型:解答题
在A、B、C、D四小题中只能选做2题,每小题10,共计20分。请在答题卡指定区域作答。解答应写出文字说明、证明过程或演算步骤。
A、选修4-1:几何证明选讲
如图,已知梯形ABCD为圆内接四边形,AD//BC,过C作该圆的切线,交AD的延长线于E,求证:ΔABC∽ΔEDC。

B、选修4-2:矩形与变换
已知 为矩阵
为矩阵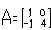 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。
C、选修4-4:坐标系与参数方程
在平面直角坐标系xoy中,曲线C的参数方程为 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为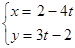 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
D、选修4-5:不等式选讲
已知a,b都是正实数,且ab=2。求证:(1+2a)(1+b)≥9。
科目:高中数学 来源:2011届江苏省南京市高三第二次模拟考试数学卷 题型:解答题
在A、B、C、D四小题中只能选做2题,每小题10,共 计20分。请在答题卡指定区域作答。解答应写出文字
计20分。请在答题卡指定区域作答。解答应写出文字 说明、证明过程或演算
说明、证明过程或演算 步骤。
步骤。
A、选修4-1:几何证明选讲
如图,已知梯形ABCD为 圆内接四边形,AD//BC,过C作该圆的切线,交AD的延长线于E,求证:ΔABC∽ΔEDC。
圆内接四边形,AD//BC,过C作该圆的切线,交AD的延长线于E,求证:ΔABC∽ΔEDC。
B、选修4-2:矩形与变换
已知 为矩阵
为矩阵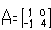 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。
C、选修4-4:坐标系与参数方程 在平面直角坐标系xoy中,曲线C的参数方程为
在平面直角坐标系xoy中,曲线C的参数方程为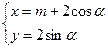 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
D、选修4-5:不等式选讲
已知a,b都是 正实数,且ab=2。求证:(1+2a)(1+b)≥9。
正实数,且ab=2。求证:(1+2a)(1+b)≥9。
科目:高中数学 来源:不详 题型:解答题
 计20分。请在答题卡指定区域作答。解答应写出文字
计20分。请在答题卡指定区域作答。解答应写出文字 说明、证明过程或演算
说明、证明过程或演算 步骤。
步骤。 圆内接四边形,AD//BC,过C作该圆的切线,交AD的延长线于E,求证:ΔABC∽ΔEDC。
圆内接四边形,AD//BC,过C作该圆的切线,交AD的延长线于E,求证:ΔABC∽ΔEDC。
 为矩阵
为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。 在平面直角坐标系xoy中,曲线C的参数方程为
在平面直角坐标系xoy中,曲线C的参数方程为 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。 正实数,且ab=2。求证:(1+2a)(1+b)≥9。
正实数,且ab=2。求证:(1+2a)(1+b)≥9。科目:高中数学 来源:2014届辽宁省分校高二12月月考理科数学试题(解析版) 题型:解答题
点A、B分别是以双曲线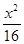
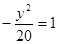 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,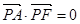
(1)求椭圆C的的方程;
(2)求点P的坐标;
(3)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值。
科目:高中数学 来源:2014届广东省高一上学期期末数学试卷 题型:解答题
设A、B是函数y= log2x图象上两点, 其横坐标分别为a和a+4, 直线l: x=a+2与函数y= log2x图象交于点C, 与直线AB交于点D。
(1)求点D的坐标;
(2)当△ABC的面积等于1时, 求实数a的值。
(3)当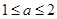 时,求△ABC的面积的取值范围。
时,求△ABC的面积的取值范围。
科目:高中数学 来源: 题型:解答题
点A、B分别是以双曲线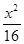
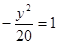 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,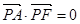
(1)求椭圆C的的方程;
(2)求点P的坐标;
(3)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值。
科目:高中数学 来源:不详 题型:解答题
 时,求△ABC的面积的取值范围。
时,求△ABC的面积的取值范围。科目:高中数学 来源:不详 题型:解答题

 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
科目:高中数学 来源:2011年高考试题数学1(江苏卷)解析版 题型:解答题
【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤.
A. 选修4-1:几何证明选讲
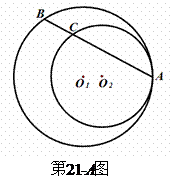 如图,圆
如图,圆 与圆
与圆 内切于点
内切于点 ,其半径分别为
,其半径分别为 与
与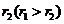 ,
,
圆 的弦
的弦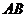 交圆
交圆 于点
于点 (
( 不在
不在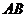 上),
上),
求证: 为定值。
为定值。
B. 选修4-2:矩阵与变换
已知矩阵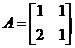 ,向量
,向量 ,求向量
,求向量 ,使得
,使得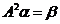 .
.
C.选修4-4:坐标系与参数方程
在平面直角坐标系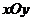 中,求过椭圆
中,求过椭圆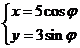 (
( 为参数)的右焦点且与直线
为参数)的右焦点且与直线 (
( 为参数)平行的直线的普通方程。
为参数)平行的直线的普通方程。
D.选修4-5:不等式选讲
解不等式: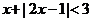
科目:高中数学 来源:0103 模拟题 题型:解答题
 (a>b>0)的左、右焦点为F1,F2,过点F1斜率为正数的直线交Γ于A,B两点,且AB⊥AF2,|AF2|,|AB|,|BF2|成等差数列。
(a>b>0)的左、右焦点为F1,F2,过点F1斜率为正数的直线交Γ于A,B两点,且AB⊥AF2,|AF2|,|AB|,|BF2|成等差数列。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com