练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，在四边形ABCD 中，E ，F 分别为AD ，BC 的中点，则=
    A.
    B.
    C.
    D.
    D
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：同步题 题型：证明题

    如图所示，在四边形ABCD 中，E ，F 分别为AD ，BC 的中点，求证：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，在四边形ABCD中，E、F分别为AD、BC的中点，试证：=（）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

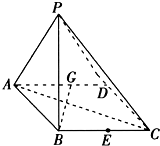    如图所示，在四棱锥P-ABCD中，底面ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所在的平面垂直于底面ABCD．
    （1）若G为AD边的中点，求证：BG⊥平面PAD；
    （2）求证：AD⊥PB；
    （3）求二面角A-BC-P的大小；
    （4）若E为BC边的中点，能否在棱PC上找一点F，使得平面DEF⊥平面ABCD？并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省、二中高三上学期期末联考文科数学卷（解析版） 题型：解答题

    如图所示，在四棱锥中，底面ABCD是边长为a的正方形，侧面底面ABCD，且，若E，F分别为PC，BD的中点．

    （1）求证：平面PAD；

    （2）求证：平面PDC平面PAD；

    （3）求四棱锥的体积．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

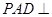    如图所示，在四棱锥中，底面ABCD是边长为a的正方形，侧面底面ABCD，且，若E，F分别为PC，BD的中点．

    （1）求证：平面PAD；
    （2）求证：平面PDC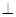平面PAD；
    （3）求四棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：证明题

    如图所示，在四棱锥S-ABCD中，底面ABCD为平行四边形，E，F分别为AB，SC的中点，求证：EF∥平面SAD。

    查看答案和解析>>

    科目：高中数学 来源：2013年高考数学备考复习卷B5：点、直线、平面之间的位置关系（解析版） 题型：解答题

    如图所示，在四棱锥P-ABCD中，底面ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所在的平面垂直于底面ABCD．
    （1）若G为AD边的中点，求证：BG⊥平面PAD；
    （2）求证：AD⊥PB；
    （3）求二面角A-BC-P的大小；
    （4）若E为BC边的中点，能否在棱PC上找一点F，使得平面DEF⊥平面ABCD？并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

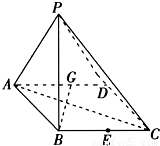
    如图所示，在正四棱柱ABCD－A1B1C1D1中，E，F，G，H分别是CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH上或其内部运动，且使MN⊥AC.

    对于下列命题：①点M可以与点H重合；②点M可以与点F重合；③点M可以在线段FH上；④点M可以与点E重合．其中真命题的序号是________(把真命题的序号都填上)．

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文复习二轮作业手册新课标·通用版限时集12讲练习卷（解析版） 题型：填空题

    如图所示，在正四棱柱ABCD－A1B1C1D1中，E，F，G，H分别是CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH上或其内部运动，且使MN⊥AC.

    对于下列命题：①点M可以与点H重合；②点M可以与点F重合；③点M可以在线段FH上；④点M可以与点E重合．其中真命题的序号是________(把真命题的序号都填上)．

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖南省永州市蓝山二中等三校高三第四次联考数学试卷（理科）（解析版） 题型：解答题

    如图所示，在直角梯形ABCD中，∠A=90°，∠C=45°，AB=2，AD=1，E是AB中点，F是DC上的点，且EF∥AD，现以EF为折痕将四边形AEFD向上折起，使平面AEFD垂直平面EBCF，连AC，DC，BA，BD，BF，

    （1）求证：CB⊥平面DFB；
    （2）求二面角B-AC-D的余弦值．

    查看答案和解析>>


    同步练习册答案