
科目:初中数学 来源:《24.1-24.3 图形的相似》2009年阶段性复习(解析版) 题型:选择题
科目:初中数学 来源: 题型:
科目:初中数学 来源:2012年浙教版初中数学八年级上2.3等腰三角形的判定练习卷(解析版) 题型:填空题
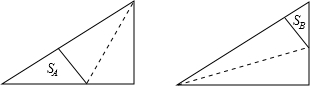
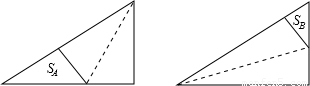
如图是两个全等的三角形纸片,其三边长之比为3:4:5,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为SA,SB,已知SA+SB=13,则纸片的面积是 .

科目:初中数学 来源:2011年河北省廊坊市三河市中考数学一模试卷(解析版) 题型:填空题
科目:初中数学 来源: 题型:填空题
科目:初中数学 来源:河北省模拟题 题型:填空题

科目:初中数学 来源: 题型:
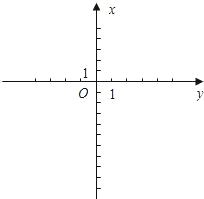 锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.
锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com