
设a>0,b>0,若a+b=ab-3,则
|
科目:高中数学 来源:云南省昆明一中2010届高三第一次月考数学(理)试题 题型:013
设a>1,集合![]() ,B={x|x2-(1+a)x+a<0}.若A
,B={x|x2-(1+a)x+a<0}.若A![]() B,则a的取值范围是
B,则a的取值范围是
A.1<a≤3
B.a≥3
C.a>3
D.1<a<3
科目:高中数学 来源:云南省昆明一中2010届高三第一次月考数学(文)试题 题型:013
设a>1,集合![]() ,B={x|x2-(1+a)x+a<0}.若A
,B={x|x2-(1+a)x+a<0}.若A![]() B,则a的取值范围是
B,则a的取值范围是
A.1<a≤3
B.a≥3
C.a>3
D.1<a<3
科目:高中数学 来源: 题型:
设a=![]() ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数![]() >0,若y=f(
>0,若y=f(![]() x)在区间
x)在区间![]() 上是增函数,求
上是增函数,求![]() 的取值范围;
的取值范围;
(3)设集合A=![]() ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A![]() B,求实数m的取值范围.
B,求实数m的取值范围.
科目:高中数学 来源: 题型:解答题
设a=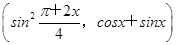 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数ω>0,若y=f(ωx)在区间 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;
(3)设集合A=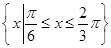 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A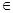 B,求实数m的取值范围.
B,求实数m的取值范围.
科目:高中数学 来源:不详 题型:解答题
 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b. 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围; ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A B,求实数m的取值范围.
B,求实数m的取值范围.科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第3课时练习卷(解析版) 题型:解答题
设a=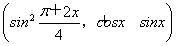 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数ω>0,若y=f(ωx)在区间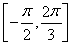 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;
(3)设集合A=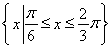 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A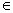 B,求实数m的取值范围.
B,求实数m的取值范围.
科目:高中数学 来源: 题型:
(1)求椭圆的方程;
(2)若直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值;
(3)试问:三角形AOB的面积是否为定值?如果是,请写出推理过程;如果不是,请说明理由.
科目:高中数学 来源:不详 题型:解答题
 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b. >0,若y=f(
>0,若y=f( x)在区间
x)在区间 上是增函数,求
上是增函数,求 的取值范围;
的取值范围; ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A B,求实数m的取值范围.
B,求实数m的取值范围.科目:高中数学 来源: 题型:
 设椭圆C:
设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| F1F2 |
| 3 |
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| QB |
| OP |
| b2 |
| a2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com