练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对任意的x1，x2∈(0，
    π
    2
    )    ，x1＜x2，y1
    1+sinx1
    x1
    ，y2=
    1+sinx2
    x2
    ；则（　　）
    A．y1＞y2B．y1＜y2C．y1=y2D．无法确定
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    对任意的x1，x2∈(0，
    π
    2
    )    ，x1＜x2，y1
    1+sinx1
    x1
    ，y2=
    1+sinx2
    x2
    ；则（　　）
    A．y1＞y2B．y1＜y2C．y1=y2D．无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对任意的x1，x2∈（0，
    π
    2
    ），x1＜x2，y1=
    1+sinx1
    x1
    ，y2=
    1+sinx2
    x2
    ；则（　　）
    A、y1＞y2
    B、y1＜y2
    C、y1=y2
    D、无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    A 任意a，b∈R，定义运算a*b=
    ab，ab≤0
    -
    a
    b
    ，ab＞0
    ，则f（x）=x*lnx的最大值为
    0
    0

    B 对于函数①f（x）=4x+
    1
    x
    -5；②f（x）=|log2x|-(
    1
    2
    )    x    ；③f（x）=cos（x+2）-cosx；
    命题甲：f（x）在区间（1，2）上是增函数；
    命题乙：f（x）在区间（0，+∞）上恰有两个零点x1，x2，且x1x2＜1．
    能使命题甲、乙均为真命题的函数序号是
    ①②
    ①②
    ．

    查看答案和解析>>

    科目：高中数学 来源：0113 期中题 题型：单选题

    下列函数f(x)中，满足“对任意的x1，x2∈(0，+∞)，当x1＜x2时，都有f(x1)＞f(x2)”的是
    [     ]
    A.
    B.f(x)=(x-1)2
    C.f(x)=ex
    D.f(x)=ln(x+1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在(0，+∞)内的函数f(x),对任意的x,y∈(0,+∞)都有f(xy)=f(x)+f(y),当且仅当x＞1时f(x)＞0成立.

    (1)设x,y∈(0,+∞),求证：f()=f(y)-f(x);

    (2)设x1,x2∈(0,+∞),f(x1)＞f(x2),试比较x1,x2的大小；

    (3)解不等式f()＞f(ax-3)(0＜a＜1).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

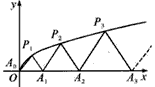
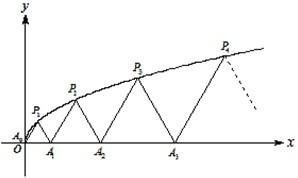    精英家教网如图，P1（x1，y1）、P2（x2，y2）、…、Pn（xn，yn）（0＜y1＜y2＜…＜yn）是曲线C：y2=3x（y≥0）上的n个点，点Ai（ai，0）（i=1，2，3，…，n）在x轴的正半轴上，且△Ai-1AiPi是正三角形（A0是坐标原点）．
    （1）写出a1，a2，a3；
    （2）求出点An（an，0）（n∈N*）的横坐标an关于n的表达式；
    （3）设bn=
    1
    an+1
    +
    1
    an+2
    +
    1
    an+3
    +…+
    1
    a2n
    ，若对任意的正整数n，当m∈[-1，1]时，不等式t2-2mt+
    1
    6
    ＞bn    恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若定义在R上的函数对任意的x1，x2∈R，都有f（x1+x2）=f（x1）+f（x2）-1成立，且当x＞0时，f（x）＞1，若f（4）=5，则不等式f（3m-2）＜3的解集为
    （-∞，
    4
    3
    ）
    （-∞，
    4
    3
    ）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知k＞0，函数数学公式
    （1）若对任意x1，x2∈[-1，1]都有f（x1）≥g（x2），求k的取值范围；
    （2）若存在x1，x2∈[-1，1]，使得f（x1）＜g（x2），求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：模拟题 题型：解答题

    如图，P1（x1，y1）、P2 （x2，y2）、…、Pn（xn，yn）（0＜y1＜y2＜…＜yn）是曲线C：y2=3x（y≥0）上的n个点，点Ai（ai，0）（i=1，2，3，…，n）在x轴的正半轴上， 且△Ai-1AiPi是正三角形（A0是坐标原点）。
    （1）写出a1、a2、a3；
    （2）求出点An（an，0）（n∈N*）的横坐标an关于n的表达式；
    （3）设，若对任意的正整数n，当m∈[-1，1]时，不等式t2-2mt+＞bn恒成立，求实数t的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：东城区模拟 题型：解答题

    如图，P1（x1，y1）、P2（x2，y2）、…、Pn（xn，yn）（0＜y1＜y2＜…＜yn）是曲线C：y2=3x（y≥0）上的n个点，点Ai（ai，0）（i=1，2，3，…，n）在x轴的正半轴上，且△Ai-1AiPi是正三角形（A0是坐标原点）．
    （1）写出a1，a2，a3；
    （2）求出点An（an，0）（n∈N*）的横坐标an关于n的表达式；
    （3）设bn=
    1
    an+1
    +
    1
    an+2
    +
    1
    an+3
    +…+
    1
    a2n
    ，若对任意的正整数n，当m∈[-1，1]时，不等式t2-2mt+
    1
    6
    ＞bn    恒成立，求实数t的取值范围．
    精英家教网

    查看答案和解析>>


    同步练习册答案