练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    定义域为R的函数f（x）对任意x都有f（2+x）=f（2-x），且其导函数f′（x）满足
    f′(x)
    2-x
    ＞0，则当2＜a＜4，有（　　）
    A．f（2a）＜f（log2a）＜f（2）B．f（log2a）＜f（2）＜f（2a）
    C．f（2a）＜f（2）＜f（log2a）D．f（log2a）＜f（2a）＜f（2）
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    定义域为R的函数f（x）对任意x都有f（2+x）=f（2-x），且其导函数f′（x）满足
    f′(x)
    x-2
    ＞0    ，则当2＜a＜4时，有（　　）
    A、f（2a）＜f（2）＜f（log2a）
    B、f（2）＜f（2a）＜f（log2a）
    C、f（2）＜f（log2a）＜f（2a）
    D、f（log2a）＜f（2a）＜f（2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义域为R的函数f（x）对任意x都有f（2+x）=f（2-x），且其导函数f′（x）满足
    f′(x)
    2-x
    ＞0，则当2＜a＜4，有（　　）
    A、f（2a）＜f（log2a）＜f（2）
    B、f（log2a）＜f（2）＜f（2a）
    C、f（2a）＜f（2）＜f（log2a）
    D、f（log2a）＜f（2a）＜f（2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义域为R的函数f（x）对任意x都有f（2+x）=f（2-x），且其导函数f′（x）满足
    f′(x)2-x
    ＞0，则当2＜a＜4时f（2a），f（2），f（log2a）的大小关系为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义域为R的函数f（x）对任意x∈R都有f（x）=f（4-x），且其导函数f′（x）满足（x-2）f′（x）＞0，则当2＜a＜4时，有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义域为R的函数f（x）对任意x都有f（x）=f（4-x），若x∈[2，+∞）时，f（x）单调递增，则当2＜a＜4时，有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

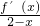    定义域为R的函数f（x）对任意x都有f（2+x）=f（2-x），且其导函数f′（x）满足数学公式＞0，则当2＜a＜4时f（2a），f（2），f（log2a）的大小关系为________．

    查看答案和解析>>

    科目：高中数学 来源：三亚模拟 题型：单选题

    定义域为R的函数f（x）对任意x都有f（2+x）=f（2-x），且其导函数f′（x）满足
    f′(x)
    2-x
    ＞0，则当2＜a＜4，有（　　）
    A．f（2a）＜f（log2a）＜f（2）B．f（log2a）＜f（2）＜f（2a）
    C．f（2a）＜f（2）＜f（log2a）D．f（log2a）＜f（2a）＜f（2）

    查看答案和解析>>

    科目：高中数学 来源：永州一模 题型：单选题

    定义域为R的函数f（x）对任意x都有f（2+x）=f（2-x），且其导函数f′（x）满足
    f′(x)
    x-2
    ＞0    ，则当2＜a＜4时，有（　　）
    A．f（2a）＜f（2）＜f（log2a）B．f（2）＜f（2a）＜f（log2a）
    C．f（2）＜f（log2a）＜f（2a）D．f（log2a）＜f（2a）＜f（2）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    定义域为R的函数f（x）对任意x∈R都有f（x）=f（4-x），且其导函数f′（x）满足（x-2）f′（x）＞0，则当2＜a＜4时，有（　　）
    A．f（2a）＜f（2）＜f（log2a）B．f（2）＜f（2a）＜f（log2a）
    C．f(2)＜f(log2a)＜f(2a)D．f(log2a)＜f(2a)＜f(2)

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省临沂市映达高考补习学校高三一轮复习期中迎考数学模拟试卷1（理科）（解析版） 题型：选择题

    定义域为R的函数f（x）对任意x都有f（x）=f（4-x），若x∈[2，+∞）时，f（x）单调递增，则当2＜a＜4时，有（ ）
    A．f（2a）＜f（2）＜f（log2a）
    B．f（2）＜f（2a）＜f（log2a）
    C．f（2）＜f（log2a）＜f（2a）
    D．f（log2a）＜f（2a）＜f（2）

    查看答案和解析>>


    同步练习册答案