练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    P是抛物线x2=
    1
    2
    (y-1)    上的动点，点A（0，-1），点M在直线PA上且分PA所成的比为2：1，则点M的轨迹方程是（　　）
    A．x2=
    1
    6
    (y+
    1
    3
    )    		B．y2=
    1
    6
    (x+
    1
    3
    )    		C．x2=
    1
    3
    (y-
    1
    3
    )    		D．x2=-
    1
    3
    (y+1)
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    P是抛物线x2=
    1
    2
    (y-1)    上的动点，点A（0，-1），点M在直线PA上且分PA所成的比为2：1，则点M的轨迹方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    P是抛物线x2=
    1
    2
    (y-1)    上的动点，点A（0，-1），点M在直线PA上且分PA所成的比为2：1，则点M的轨迹方程是（　　）
    A．x2=
    1
    6
    (y+
    1
    3
    )    		B．y2=
    1
    6
    (x+
    1
    3
    )    		C．x2=
    1
    3
    (y-
    1
    3
    )    		D．x2=-
    1
    3
    (y+1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知过点A（-4，0）的动直线l与抛物线C：x2=2py（p＞0）相交于B、C两点．当l的斜率是
    1
    2
    时，
    AC
    =4
    AB
    ．
    （1）求抛物线C的方程；
    （2）设BC的中垂线在y轴上的截距为b，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：宁德模拟 题型：解答题

    已知过点A（-4，0）的动直线l与抛物线C：x2=2py（p＞0）相交于B、C两点．当l的斜率是
    1
    2
    时，
    AC
    =4
    AB
    ．
    （1）求抛物线C的方程；
    （2）设BC的中垂线在y轴上的截距为b，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法正确的是（　　）
    A、△ABC中，已知A（1，1），B（4，1），C（2，3），则AB边上的高的方程是x=2
    B、方程y=x2（x≥0）的曲线是抛物线
    C、已知平面上两定点A、B，动点P满足|PA|-|PB|=
    1
    2
    |AB|，则P点的轨迹是双曲线
    D、第一、三象限角平分线的方程是y=x

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一青蛙从点A0（x0，y0）开始依次水平向右和竖直向上跳动，其落点坐标依次是Ai（xi，yi）（i∈N*），（如图所示，A0（x0，y0）坐标以已知条件为准），Sn表示青蛙从点A0到点An所经过的路程．
    （1）若点A0（x0，y0）为抛物线y2=2px（p＞0）准线上一点，点A1，A2均在该抛物线上，并且直线A1A2经过该抛物线的焦点，证明S2=3p．
    （2）若点An（xn，yn）要么落在y=x所表示的曲线上，要么落在y=x2所表示的曲线上，并且A0(
    1
    2
    ，
    1
    2
    )    ，试写出
    lim
    n→+∞
    Sn    （不需证明）；
    （3）若点An（xn，yn）要么落在y=2
    		1+8x
    -1    所表示的曲线上，要么落在y=2
    		1+8x
    +1    所表示的曲线上，并且A0（0，4），求Sn的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

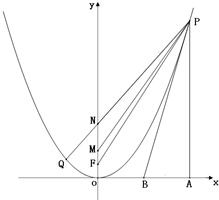    精英家教网已知四点O（0，0），F(0，
    1
    2
    )    ，M（0，1），N（0，2）．点P（x0，y0）在抛物线x2=2y上
    （Ⅰ）当x0=3时，延长PN交抛物线于另一点Q，求∠POQ的大小；
    （Ⅱ）当点P（x0，y0）（x0≠0）在抛物线x2=2y上运动时，
    ⅰ）以MP为直径作圆，求该圆截直线y=
    1
    2
    所得的弦长；
    ⅱ）过点P作x轴的垂线交x轴于点A，过点P作该抛物线的切线l交x轴于点B．问：是否总有∠FPB=∠BPA？如果有，请给予证明；如果没有，请举出反例．

    查看答案和解析>>


    同步练习册答案