对任意两个不相等的实数a，b，定义在R上的函数f（x）总有

f(a)-f(b)

b-a

＞0成立，则必有（　　）

A．f（a）＞f（b）	B．f（a）＜f（b）
C．f（x）在R上是增函数	D．f（x）在R上是减函数

相关习题

科目：高中数学 来源： 题型：

对任意两个不相等的实数a，b，定义在R上的函数f（x）总有

f(a)-f(b)

b-a

＞0成立，则必有（　　）

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

对任意两个不相等的实数a，b，定义在R上的函数f（x）总有

f(a)-f(b)

b-a

＞0成立，则必有（　　）

A．f（a）＞f（b）	B．f（a）＜f（b）
C．f（x）在R上是增函数	D．f（x）在R上是减函数

查看答案和解析>>

科目：高中数学 来源：2012-2013学年浙江省舟山市岱山县大衢中学高一（上）10月月考数学试卷（解析版） 题型：选择题

对任意两个不相等的实数a，b，定义在R上的函数f（x）总有

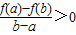成立，则必有（）
A．f（a）＞f（b）
B．f（a）＜f（b）
C．f（x）在R上是增函数
D．f（x）在R上是减函数

查看答案和解析>>

科目：高中数学 来源： 题型：单选题

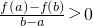对任意两个不相等的实数a，b，定义在R上的函数f（x）总有 $数学公式$ 成立，则必有

A.
f（a）＞f（b）
B.
f（a）＜f（b）
C.
f（x）在R上是增函数
D.
f（x）在R上是减函数

查看答案和解析>>

科目：高中数学 来源： 题型：

已知函数对于任意两个不相等的实数_l，₂，都有(_l+₂)=(₁)f(₂)成立，且(0)≠0 则(一2007)(一2006)(一2005)……(2005)(2006)(2007)的值是

A．0 B．1 C．2 D．3

查看答案和解析>>

科目：高中数学 来源：重庆市一中09-10学年高一10月月考 题型：选择题

若对任意的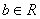，关于的一元二次方程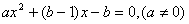都恒有两个不相等的实数根，则实数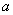的取值范围是（）

A. B. C. D.

查看答案和解析>>

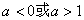
科目：高中数学 来源：上海高考真题 题型：解答题

若实数x、y、m满足|x-m|＞|y-m|，则称x比y远离m，
(Ⅰ)若x²-1比1远离0，求x的取值范围；
(Ⅱ)对任意两个不相等的正数a、b，证明：a³+b³比a²b+ab²远离2ab

；
(Ⅲ)已知函数f(x)的定义域D={x|x≠

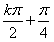，k∈Z，x∈R}，任取x∈D，f(x)等于sinx和cosx中远离0的那个值．写出函数f(x)的解析式，并指出它的基本性质(结论不要求证明)．

查看答案和解析>>

科目：高中数学 来源： 题型：

若实数x、y、m满足|x﹣m|＜|y﹣m|，则称x比y接近m．

（1）若x²﹣1比3接近0，求x的取值范围；

（2）对任意两个不相等的正数a、b，证明：a²b+ab²比a³+b³接近；

（3）已知函数f（x）的定义域D{x|x≠kπ，k∈Z，x∈R}．任取x∈D，f（x）等于1+sinx和1﹣sinx中接近0的那个值．写出函数f（x）的解析式，并指出它的奇偶性、最小正周期、最小值和单调性（结论不要求证明）．

查看答案和解析>>

科目：高中数学 来源：陕西省月考题 题型：解答题

若实数x、y、m满足|x﹣m|＜|y﹣m|，则称x比y接近m．
（1）若2x﹣1比3接近0，求x的取值范围；
（2）对任意两个不相等的正数a、b，证明：a²b+ab²比a³+b³接近

．

查看答案和解析>>

科目：高中数学 来源：江苏省阜宁县中学2011－2012学年高二下学期期中调研考试数学试题 题型：044

若实数x，y，m满足|x－m|＜|y－m|，则称x比y接近m，

(1)若x²－1比3接的0，求x的取值范围．

(2)对任意两个不相等的正数a，b，证明：a²b＋ab²比a³＋b³接近2ab．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学

对任意两个不相等的实数a，b，定义在R上的函数f（x）总有 $数学公式$ 成立，则必有