科目：高中数学 来源：2013年广东省广州市高考数学二模试卷（文科）（解析版） 题型：选择题

如果函数f（x）=ln（-2x+a）的定义域为（-∞，1），则实数a的值为（）
A．-2
B．-1
C．1
D．2

查看答案和解析>>

科目：高中数学 来源：广州二模 题型：单选题

如果函数f（x）=ln（-2x+a）的定义域为（-∞，1），则实数a的值为（　　）

A．-2

B．-1

C．1

D．2

查看答案和解析>>

科目：高中数学 来源： 题型：单选题

如果函数f（x）=ln（-2x+a）的定义域为（-∞，1），则实数a的值为

A.
-2
B.
-1
C.
1
D.
2

查看答案和解析>>

科目：高中数学 来源： 题型：

（2013•广州二模）如果函数f（x）=ln（-2x+a）的定义域为（-∞，1），则实数a的值为（　　）

A．-2

B．-1

C．1

D．2

查看答案和解析>>

科目：高中数学 来源： 题型：

定义在（-∞，0）∪（0，+∞）上的函数f（x），如果对于任意给定的等比数列{a_n}，{f（a_n）}仍是等比数列，则称f（x）为“保等比数列函数”。现有定义在（-∞，0）∪（0，+∞）上的如下函数：①f（x）=x²；②f（x）=2^x；③；④f（x）=ln|x |。

则其中是“保等比数列函数”的f（x）的序号为

A.①② B.③④ C.①③ D.②④

查看答案和解析>>

科目：高中数学 来源：2012-2013学年浙江省绍兴市高一下学期期中考试文科数学试卷（解析版） 题型：选择题

定义在（-∞，0）∪（0，+∞）上的函数f（x），如果对于任意给定的等比数列{a_n}，{f（a_n）}仍是等比数列，则称f（x）为“保等比数列函数”。现有定义在（）

（-∞，0）∪（0，+∞）上的如下函数：①f（x）=x²；②f（x）=2^x；③；④f（x）="ln|x" |。则其中是“保等比数列函数”的f（x）的序号为（）

A．①② B．①③ C．③④ D．②④

查看答案和解析>>

科目：高中数学 来源：2014届山西省高二暑假考试数学试卷（解析版） 题型：选择题

定义在（-∞，0）∪（0，+∞）上的函数f（x），如果对于任意给定的等比数列{a_n}，{f（a_n）}仍是等比数列，则称f（x）为“保等比数列函数”。现有定义在（-∞，0）∪（0，+∞）上的如下函数：①f（x）=x²；②f（x）=2^x；③；④f（x）=ln|x |。

则其中是“保等比数列函数”的f（x）的序号为( )

A.①② B.③④ C.①③ D.②④

查看答案和解析>>

科目：高中数学 来源： 题型：单选题

定义在（-∞，0）∪（0，+∞）上的函数f（x），如果对于任意给定的等比数列{a_n}，{f（a_n）}仍是等比数列，则称f（x）为“保等比数列函数”。现有定义在（）
（-∞，0）∪（0，+∞）上的如下函数：①f（x）=x²；②f（x）=2^x；③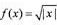；④f（x）="ln|x" |。则其中是“保等比数列函数”的f（x）的序号为（）