练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设集合A={x|x=kπ+（-1）k
    π
    2
    ，k∈Z}，B={x|x=2kπ+
    π
    2
    ，k∈Z}，则集合A与B之间的关系为（　　）
    A．A?BB．A?BC．A=BD．A∩B=φ
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    设集合A={x|x=kπ+（-1）k
    π
    2
    ，k∈Z}，B={x|x=2kπ+
    π
    2
    ，k∈Z}，则集合A与B之间的关系为（　　）
    A、A?BB、A?B
    C、A=BD、A∩B=φ

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设集合A={x|x=kπ+（-1）k
    π
    2
    ，k∈Z}，B={x|x=2kπ+
    π
    2
    ，k∈Z}，则集合A与B之间的关系为（　　）
    A．A?BB．A?BC．A=BD．A∩B=φ

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    设A＝{x｜x＝2k，k∈Z}，B＝{x｜x＝2k＋1，k∈Z}，C＝{x｜x＝2（k＋1），k∈Z}，D＝{x｜x＝2k－1，k∈Z}，在A、B、C、D中，哪些集合相等，哪些集合的交集是空集?

     

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    设A＝{x｜x＝2k，k∈Z}，B＝{x｜x＝2k＋1，k∈Z}，C＝{x｜x＝2（k＋1），k∈Z}，D＝{x｜x＝2k－1，k∈Z}，在A、B、C、D中，哪些集合相等，哪些集合的交集是空集?

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    下列说法正确的有
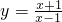    ①集合A={x∈z|x=2k+1，k∈z}与集合B={x|x=2k-1，k∈z}是相等集合；②设集合A={x|（x-3）（x-a）=0，a∈R}，B={x|x2-5x+4=0}，则A∪B={1，3，4，a}；③函数数学公式在区间[2，6]上的最大值为3；④函数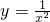数学公式在定义域上是减函数．


    1. A.
      1个
    2. B.
      2个
    3. C.
      3个
    4. D.
      4个

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖南师大附中高一（上）12月月考数学试卷（解析版） 题型：选择题

    下列说法正确的有（ ）
    ①集合A={x∈z|x=2k+1，k∈z}与集合B={x|x=2k-1，k∈z}是相等集合；②设集合A={x|（x-3）（x-a）=0，a∈R}，B={x|x2-5x+4=0}，则A∪B={1，3，4，a}；③函数在区间[2，6]上的最大值为3；④函数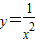在定义域上是减函数．
    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖南省长沙市高三第四次月考文科数学试卷 题型：解答题

    （本小题满分12分）设函数.

    （1）求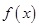的最大值，并求取得最大值时x的取值集合；

    （2）记的内角A、B、C的对边分别为a，b，c，若，b=1，c=，求a的值.[来源:Z+xx+k.Com]

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法正确的有（　　）
    ①集合A={x∈z|x=2k+1，k∈z}与集合B={x|x=2k-1，k∈z}是相等集合；②设集合A={x|（x-3）（x-a）=0，a∈R}，B={x|x2-5x+4=0}，则A∪B={1，3，4，a}；③函数y=
    x+1
    x-1
    在区间[2，6]上的最大值为3；④函数y=
    1
    x2
    在定义域上是减函数．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年重庆市杨家坪中学高三（上）11月月考数学试卷（理科）（解析版） 题型：解答题

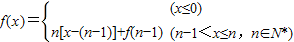    已知函数数列{an}满足an=f（n）（n∈N*）
    （1）求数列{an}的通项公式；
    （2）设x轴、直线x=a与函数y=f（x）的图象所围成的封闭图形的面积为S（a）（a≥0），求S（n）-S（n-1）（n∈N*）；
    （3）在集合M={N|N=2k，k∈Z，且1000≤k＜1500}中，是否存在正整数N，使得不等式an-1005＞S（n）-S（n-1）对一切n＞N恒成立？若存在，则这样的正整数N共有多少个？并求出满足条件的最小的正整数N；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数F(x)=kx2-2
    		4+2m-m2
    x    ，G(x)=-
    		1-(x-k)2
    (m，k∈R)
    （1）若m，k是常数，问当m，k满足什么条件时，函数F（x）有最大值，并求出F（x）取最大值时x的值；
    （2）是否存在实数对（m，k）同时满足条件：（甲）F（x）取最大值时x的值与G（x）取最小值的x值相同，（乙）k∈Z？
    （3）把满足条件（甲）的实数对（m，k）的集合记作A，设B={（m，k）|k2+（m-1）2≤r2，r＞0}，求使A⊆B的r的取值范围．

    查看答案和解析>>


    同步练习册答案