练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知直线l与直线m是异面直线，直线l在平面α内，在过直线m所作的所有平面中，下列结论正确的是（　　）
    A．一定存在与l平行的平面，也一定存在与α平行的平面
    B．一定存在与l平行的平面，也一定存在与α垂直的平面
    C．一定存在与l垂直的平面，也一定存在与α平行的平面
    D．一定存在与l垂直的平面，也一定存在与α垂直的平面
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：广西北海市合浦县教育局2010-2011学年高二下学期期末考试数学试题 题型：013

    已知直线l与直线m是异面直线，直线l在平面α内，在过直线m所作的所有平面中，下列结论正确的是

    [　　]
    A．

    一定存在与l平行的平面，也一定存在与α平行的平面；

    B．

    一定存在与l平行的平面，也一定存在与α垂直的平面；

    C．

    一定存在与l垂直的平面，也一定存在与α平行的平面；

    D．

    一定存在与l垂直的平面，也一定存在与α垂直的平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，已知圆x2+y2=1与x轴正半轴的交点为F，AB为该圆的一条弦，直线AB的方程为x=m．记以AB为直径的圆为⊙C，记以点F为右焦点、短半轴长为b（b＞0，b为常数）的椭圆为D．
    （1）求⊙C和椭圆D的标准方程；
    （2）当b=1时，求证：椭圆D上任意一点都不在⊙C的内部；
    （3）已知点M是椭圆D的长轴上异于顶点的任意一点，过点M且与x轴不垂直的直线交椭圆D于P、Q两点（点P在x轴上方），点P关于x轴的对称点为N，设直线QN交x轴于点L，试判断
    OM
    •
    OL
    是否为定值？并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

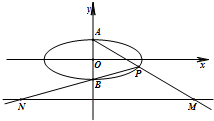    在平面直角坐标系xOy中，如图，已知椭圆C：
    x24
    +y2    =1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、BP与直线l：y=-2分别交于点M、N；
    （I）设直线AP、BP的斜率分别为k1，k2求证：k1•k2为定值；
    （Ⅱ）求线段MN长的最小值；
    （Ⅲ）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，已知椭圆E：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的离心率为
    		2
    2
    ，左焦点为F，过原点的直线l交椭圆于M，N两点，△FMN面积的最大值为1．
    （1）求椭圆E的方程；
    （2）设P，A，B是椭圆E上异于顶点的三点，Q（m，n）是单位圆x2+y2=1上任一点，使
    OP
    =m
    OA
    +n
    OB
    ．
    ①求证：直线OA与OB的斜率之积为定值；
    ②求OA2+OB2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知l、m、n是直线，α、β是平面，给出命题：

    ①若m∥α，n∥α，则m∥n；

    ②设α-l-β是直二面角，若m⊥l，则m⊥β；

    ③若m、n在α内的射影依次为一个点和一条直线，且m⊥n，则nα或n∥α；

    ④设m、n是异面直线，若m∥α，则n与α相交.

    其中真命题的序号是___________(把所有真命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知l、m、n是直线，α、β是平面，给出命题：

    ①若m∥α，n∥α，则m∥n；

    ②设α-l-β是直二面角，若m⊥l，则m⊥β；

    ③若m、n在α内的射影依次为一个点和一条直线，m⊥n，则nα或n∥α；

    ④设m、n是异面直线，若m∥α，则n与α相交．

    其中真命题的序号是___________.(把所有真命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏五校高三下学期期初教学质量调研数学卷（解析版） 题型：解答题

    在平面直角坐标系xOy中，如图，已知椭圆C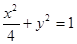：的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、PB与直线l：y＝－2分别交于点M、N.

    （1）设直线AP、PB的斜率分别为k1，k2，求证：k1·k2为定值；

    （2）求线段MN长的最小值；

    （3）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在平面直角坐标系xOy中，如图，已知椭圆C：的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、PB与直线l：y＝－2分别交于点M、N.

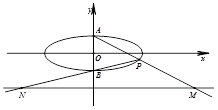
    （1）设直线AP、PB的斜率分别为k1，k2，求证：k1·k2为定值；
    （2）求线段MN长的最小值；
    （3）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知平面α，β，γ，直线l，m，点A，在下面四个命题中正确的是（　　）
    A．若 l?α，m∩α=A，则l与m必为异面直线
    B．若 l∥α，l∥m，则 m∥α
    C．若 l?α，m?β，l∥β，m∥α，则 α∥β
    D．若 α⊥γ，α∩γ=m，γ∩β=l，l⊥m，则 l⊥α

    查看答案和解析>>

    科目：高中数学 来源：东莞一模 题型：解答题

    在平面直角坐标系xOy中，已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左焦点为F1（-1，0），且椭圆C的离心率e=
    1
    2
    ．
    （1）求椭圆C的方程；
    （2）设椭圆C的上下顶点分别为A1，A2，Q是椭圆C上异于A1，A2的任一点，直线QA1，QA2分别交x轴于点S，T，证明：|OS|•|OT|为定值，并求出该定值；
    （3）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=2与圆O：x2+y2=
    16
    7
    相交于不同的两点A、B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

    查看答案和解析>>


    同步练习册答案