
【题目】二次函数y=ax2﹣bx+b(a>0,b>0)图象的顶点的纵坐标不大于 ![]() ,且图象与x轴交于A,B两点,则线段AB长度的最小值是 .
,且图象与x轴交于A,B两点,则线段AB长度的最小值是 .
【答案】2 ![]()
【解析】解:∵抛物线顶点横坐标为x=﹣ ![]() =
= ![]() ,
,
代入得:y=a ![]() ﹣
﹣ ![]() =b≤﹣
=b≤﹣ ![]() ,
,
化简得: ![]() ≥3,即b≥6a,(此时△>0,符合题意)
≥3,即b≥6a,(此时△>0,符合题意)
∵当y=ax2﹣bx+b=0,时,x1= ![]() ,x2=
,x2= ![]() ,
,
∴AB= ![]() ,
,
∵a、b均大于0,
∴当b=6a时,AB有最小值为2 ![]() ,
,
所以答案是 2 ![]() .
.
【考点精析】掌握二次函数的性质和二次函数的最值是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2019,最少经过( )次操作.
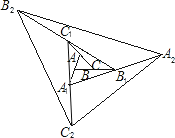
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
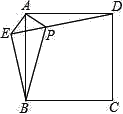
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距50千米.星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发小时时,行进中的两车相距8千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空.如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD,理由如下:
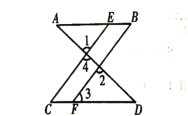
解:因为∠1=∠2(已知),且∠1=∠4( )
所以∠2=∠4(等量代换)
所以CE∥BF( )
所以∠ =∠3( )
又因为∠B=∠C(已知),所以∠3=∠B( )
所以AB∥CD ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种阳台户外伸缩晾衣架,侧面示意图如图2所示,其支架AB,CD,EF,GH,BE,DG,FK的长度都为40cm(支架的宽度忽略不计),四边形BQCP、DMEQ、FNGM是互相全等的菱形,当晾衣架的A端拉伸到距离墙壁最远时,∠B=∠D=∠F=80°,这时A端到墙壁的距离约为cm.
(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com