
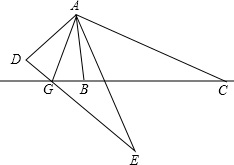
 如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.
如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.  阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
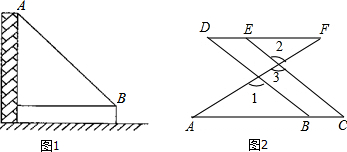
 已知,如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF,
已知,如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数据4,6,5,2,-1的中位数是4 | |
| B. | 从2,3,4,5,6中随机抽一个数,是奇数的可能性比较大 | |
| C. | 若甲组数据的方差S甲2=0.71,乙组数据的方差S乙2=0.92,则甲组数据比乙组数据小 | |
| D. | 若某种游戏活动的中奖率为35%,则参加这种活动100次必有35次中奖 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com