【题目】已知关于x的一元二次方程x2+2（k+1）x+k2+2=0有两个实根x1，x2．
（1）求实数k的取值范围；
（2）若实数k能使x1﹣x2=2
，求出k的值．
【答案】（1）k≥
（2）3
【解析】试题分析：（1）根据方程的系数结合根的判别式△≥0，即可得出关于k的一元一次不等式，解之即可得出实数k的取值范围；
（2）根据根与系数的关系可得出x1+x2=﹣2（k+1）、x1x2=k2+2，结合（x1﹣x2）2=（x1+x2）2﹣4x1x2=（2
）2，即可得出关于k的一元一次方程，解之即可得出结论．
试题解析：解：（1）∵原方程有两个实数根，∴△=[2（k+1）]2﹣4（k2+2）＞0，解得：k≥．
（2）∵x1、x2是方程x2+2（k+1）x+k2+2=0有两个实根，∴x1+x2=﹣2（k+1），x1x2=k2+2，∴（x1﹣x2）2=（x1+x2）2﹣4x1x2=（2）2，∴[﹣2（k+1）]2﹣4（k2+2）=20，即8k﹣24=0，解得：k=3．
∵k＞，∴k的值为3．
科目：初中数学 来源： 题型：
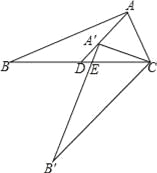
【题目】如图，Rt△ABC中，∠BAC=90°，将△ABC绕点C逆时针旋转，旋转后的图形是△A′B′C，点A的对应点A′落在中线AD上，且点A′是△ABC的重心，A′B′与BC相交于点E，那么BE：CE= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“端午节”期间，小明一家自驾游去了离家200km的某地，如图是他们离家的距离y（km）与汽车行驶时间x（h）之间的函数图象．根据图象，解答下列问题：
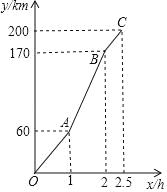
（1）点A的实际意义是 ；
（2）求出线段AB的函数表达式；
（3）他们出发2.3h时，距目的地还有多少km？
查看答案和解析>>
科目：初中数学 来源： 题型：
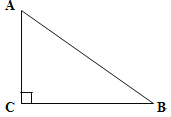
【题目】如图，已知△ABC，∠C=90，AC<BC，D为BC上一点，且到A，B两点的距离相等.
（1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；
（2）连结AD，若∠B=37°，则∠CAD=_________度.
查看答案和解析>>
科目：初中数学 来源： 题型：
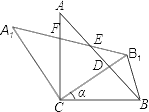
【题目】如图，△ABC中，∠ACB＝90，AC＝BC，将△ABC绕点C逆时针旋转α角（0＜α＜90）得到△A1B1C，连结BB1.设CB1交AB于D，A1B1分别交AB、AC于E、F，
（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以证明（△ABC与△A1B1C全等除外）；
（2）当△BB1D是等腰三角形时，求α.
查看答案和解析>>
科目：初中数学 来源： 题型：
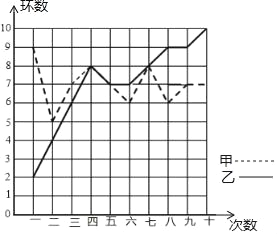
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：
（1）请将下表补充完整：（参考公式：方差S2=
[（x1﹣
）2+（x2﹣）2+…+（xn﹣）2]）
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
（2）请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看， 的成绩好些；
②从平均数和中位数相结合看， 的成绩好些；
③若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE＝
∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．
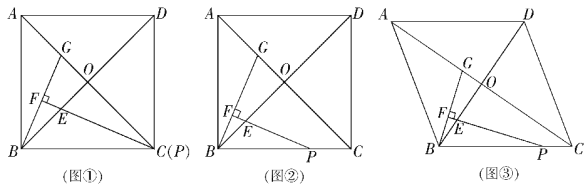
（1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；（4分）
（2）通过观察、测量、猜想：
= ，并结合图②证明你的猜想；（5分）
（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α，求的值．（用含α的式子表示）（5分）
查看答案和解析>>
科目：初中数学 来源： 题型：
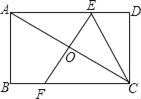
【题目】如图，矩形ABCD中，AB＝2，BC＝4，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，则△DCE的面积为（ ）
A. 
B. 
C. 2D. 1
查看答案和解析>>
科目：初中数学 来源： 题型：
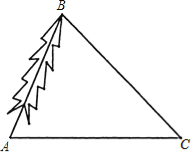
【题目】为了对一棵倾斜的古杉树AB进行保护，需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，求这棵古杉树AB的长度．（结果取整数）
参考数据：
≈1.41，sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com