
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过点A,B.
经过点A,B.
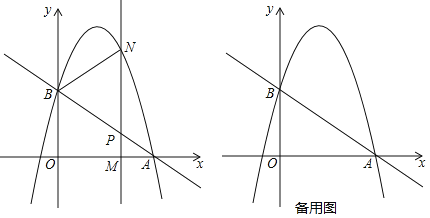
(1)求点B的坐标和抛物线的解析式;
(2)设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①求PN的最大值;
②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.
【答案】(1)点B的坐标为![]() ;抛物线的解析式为
;抛物线的解析式为![]() ;(2)①PN的最大值为3;②若以B,P,N为顶点的三角形与△APM相似,点M的坐标为
;(2)①PN的最大值为3;②若以B,P,N为顶点的三角形与△APM相似,点M的坐标为![]() 或
或![]() .
.
【解析】
(1)先将点A坐标代入直线解析式求出c的值,从而可求得B点坐标;再由A、B两点的坐标,利用待定系数法即可求得抛物线的解析式;
(2)①利用点M坐标、直线解析式、抛物线的解析式可求出点P、N的坐标,从而可求得PN用m表示的代数式,利用二次函数的性质求最大值即可;
②要使![]() 和
和![]() 相似,则需分
相似,则需分![]() 和
和![]() 两种情况讨论,然后利用相似三角形对应线段成比例求解即可.
两种情况讨论,然后利用相似三角形对应线段成比例求解即可.
(1)将![]() 代入
代入![]() 得
得![]() ,解得
,解得![]()
则直线的解析式为![]()
令![]() ,代入得
,代入得![]()
则点B的坐标为![]()
将![]() 代入抛物线
代入抛物线![]() 得:
得:
![]() ,解得
,解得
则抛物线的解析式为![]() ;
;
(2)①由题意得:点P、N的横坐标均为m,且![]()
分别代入两个解析式可得两个点的坐标为:![]()
则![]()
当![]() 时,PN随m的增大而增大;当
时,PN随m的增大而增大;当![]() 时,PN随m的增大而减小
时,PN随m的增大而减小
则当![]() 时,PN取得最大值,最大值为3;
时,PN取得最大值,最大值为3;
②在![]() 和
和![]() 中,
中,![]()
如果![]() 和
和![]() 相似,则
相似,则![]() 或
或![]()
当![]() 时,
时,![]() ,
,![]()
![]() 即
即
解得:![]() (舍去)或
(舍去)或![]()
经检验,![]() 是方程的解
是方程的解
则点M的坐标为![]()
当![]() 时,
时,![]()
![]()
由![]() 和两点距离公式可得:
和两点距离公式可得:
![]()
![]()
代入得: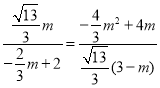 ,解得:
,解得:![]() (舍去)或
(舍去)或![]()
经检验,![]() 是方程的解
是方程的解
则点M的坐标为![]()
综上,若以B,P,N为顶点的三角形与![]() 相似,点M的坐标为
相似,点M的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】有四张背面完全相同的卡片,正面上分别标有数字﹣2,﹣1,1,2.把这四张卡片背面朝上,随机抽取一张,记下数字为m;放回搅匀,再随机抽取一张卡片,记下数字为n,则y=mx+n不经过第三象限的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:如调整价格,每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,如何定价才能使利润最大?这个最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
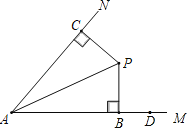
【题目】如图,点P在∠MAN内,PA平分∠MAN,PB⊥AM于点B,PC⊥AN于点C,点D是射线AM上点B右侧的一个定点.
(1)作经过A,P,D三点的圆;(保留作图痕进,不写作法)
(2)设圆与AN交于点E,∠MAN=60°,PA=4,求AE+AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游客乘坐“金碧皇宫号游船”在长江和嘉陵江的交汇处A点,测得来福土最高楼顶点F的仰角为45°,此时他头项正上方146米的点B处有架航拍无人机测得来福士最高楼顶点F的仰角为31°,游船朝码头方向行驶120米到达码头C,沿坡度i=1:2的斜坡CD走到点D,再向前走160米到达来福士楼底E,则来福士最高楼EF的高度约为( )(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.87,tan31°≈0.60)
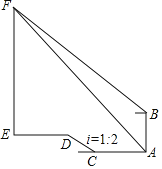
A.301.3米B.322.5米C.350.2米D.418.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com