
【题目】如图,点P在∠MAN内,PA平分∠MAN,PB⊥AM于点B,PC⊥AN于点C,点D是射线AM上点B右侧的一个定点.
(1)作经过A,P,D三点的圆;(保留作图痕进,不写作法)
(2)设圆与AN交于点E,∠MAN=60°,PA=4,求AE+AD的值.
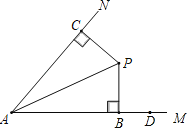
【答案】(1)见解析;(2)4![]()
【解析】
(1)作AP和AD的垂直平分线,两条直线的交点即为过A、P、D三点的圆心;
(2)连接PE、PD证明△PCE与△PBD全等即可求解.
解:(1)如图所示:
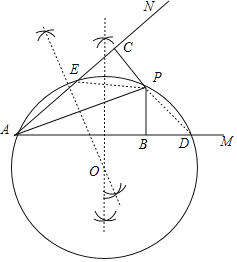
作AP和AD的垂直平分线,两条线相交于点O,
以点为圆心,OA为半径的圆即为所求作的图形;
(2)连接PE、PD,
∵PA平分∠MAN,PB⊥AD于点B,PC⊥AN于点C,
∴PB=PC,
在圆中,∵∠EAP=∠DAP,
∴PE=PD,
在△PCE和△PBD中,
∵∠PCE=∠PBD=90°,PB=PC,PE=PD.
∴Rt△PCE≌Rt△PBD(HL).
∴CE=BD.
∵∠MAN=60°,PA平分∠MAN,
∴∠PAB=30°,PA=4,
∴AB=2![]() ,
,
∴AE+AD=2AB=4![]() .
.


科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3.
(1)求二次函数的顶点坐标;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
x | … | … | |||||
y | … | … |
(4)当﹣3<x<0时,则y的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则M的坐标为( )
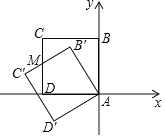
A.(1,![]() )B.(﹣1,
)B.(﹣1,![]() )C.(1,
)C.(1,![]() )D.(﹣1,
)D.(﹣1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过点A,B.
经过点A,B.
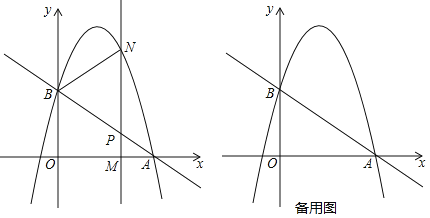
(1)求点B的坐标和抛物线的解析式;
(2)设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①求PN的最大值;
②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.
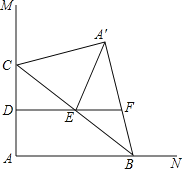
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
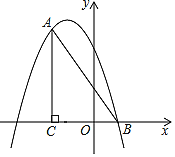
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆,别称“山城”、“雾都”,旅游资源丰富,自然人文旅游景点独具特点.近年来,重庆以其独特“3D魔幻”般的城市魅力吸引了众多海内外游客,成为名副其实的旅游打卡网红城市.某中学想了解该校九年级1200名学生对重庆自然人文旅游景点的了解情况,从九(1)、九(2)班分别抽取了30名同学进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:
a.测试成绩分成5组,其中A组:50<x≤60,B组:60<x≤70,C组:70<x≤80,D组:80<x≤90,E组:90<x≤100.测试成绩统计图如下:
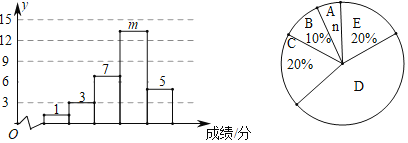
b.九(2)班D组的测试成绩分别是:81、82、82、83、84、85、86、87、88、89、89、90、90、90.
c.九(1)(2)班测试成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
九(1) | 84.2 | 84 | 89 |
九(2) | 84.6 | π | 90 |
根据以上信息,回答下列问题:
(1)根据题意,直接写出m,n的值:m= ,n= ;九(2)班测试成绩扇形统计图中A组的圆心角α= °;
(2)在此次测试中,你认为 班的学生对重庆自然人文景点更了解(填“九(1)”或“九(2)”),请说明理由(一条理由即可): ;
(3)假设该校九年级学生都参加此次测试,测试成绩大于90分为优秀,请估计该校九年级对重庆自然人文景点的了解达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com