
����Ŀ��ij�οͳ�������̻ʹ����δ����ڳ����ͼ��꽭�Ľ��㴦A�㣬������������¥����F������Ϊ45������ʱ��ͷ�����Ϸ�146�ĵ�B���мܺ������˻��������ʿ���¥����F������Ϊ31�����δ�����ͷ������ʻ120������ͷC�����¶�i��1��2��б��CD�ߵ���D������ǰ��160��������ʿ¥��E��������ʿ���¥EF�ĸ߶�ԼΪ���������������ȷ��0.1���ο����ݣ�sin31���0.52��cos31���0.87��tan31���0.60��
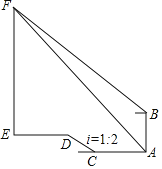
A.301.3��B.322.5��C.350.2��D.418.5��
���𰸡�B
��������
������֪�ǵ����Ǻ�������ֱ�������μ�����⣮
��ͼ��ʾ��
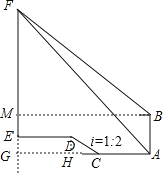
�ӳ�AC��FE���ڵ�G������B��BM��FE�ڵ�M����DH��AG�ڵ�H��
�þ���ABMG��DHEG��
��DH��x����HC��2x��
BM��AG��160+120+2x��280+2x��
EG��DH��x��
�ߡ�FAG��45������FGA��90�������AFG��45����
��FG��AG��
EF��FG��EG��AG��EG��280+2x��x��280+x��
��FM��FG��MG��280+2x��146��134+2x��
��Rt��FBM��tan31����![]() ��
��
��![]() ��0.6��
��0.6��
���x��42.5����EF��280+x��322.5��
��ѡ��B��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
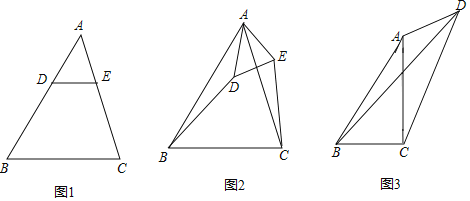
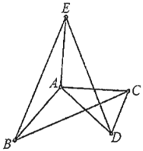
����Ŀ����1����ͼ1������ABC�У�AB��AC����D��E�ֱ��ڱ�AB��AC�ϣ���DE��BC����AD��2��AE��![]() ����
����![]() ��ֵ���� ����
��ֵ���� ����
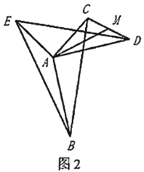
��2����ͼ2���ڣ�1���������£�����ADE�Ƶ�A��ʱ�뷽����תһ���ĽǶȣ�����CE��BD��![]() ��ֵ�仯�����仯����˵�����ɣ������仯������������ֵ��
��ֵ�仯�����仯����˵�����ɣ������仯������������ֵ��
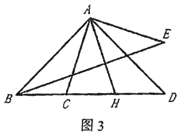
��3����ͼ3�����ı���ABCD�У�AC��BC�ڵ�C����BAC����ADC��������tan����![]() ����CD��6��AD��3ʱ����ֱ��д���߶�BD�ij��ȣ�
����CD��6��AD��3ʱ����ֱ��д���߶�BD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��x�ύ�ڵ�A(3,0)����y�ύ�ڵ�B��������
��x�ύ�ڵ�A(3,0)����y�ύ�ڵ�B��������![]() ������A��B��
������A��B��
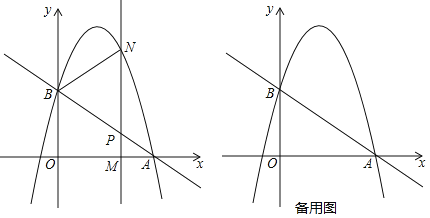
��1�����B������������ߵĽ���ʽ��
��2�����M(m,0)Ϊ�߶�OA��һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N.
����PN�����ֵ��
������B��P��NΪ���������������APM���ƣ���ֱ��д����M������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
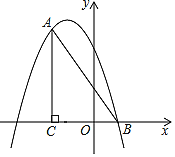
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ACB=90�㣬OC=2OB��tan��ABC=2����B������Ϊ��1��0����������y=��x2+bx+c����A��B���㣮
��1���������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ��������ϵ�һ�㣬����P��PD��ֱx���ڵ�D�����߶�AB�ڵ�E��ʹPE=![]() DE��
DE��
�����P�����ꣻ
����ֱ��PD���Ƿ���ڵ�M��ʹ��ABMΪֱ�������Σ������ڣ�����������������е�M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��y��Ľ���ΪA�������ߵĶ���Ϊ
��y��Ľ���ΪA�������ߵĶ���Ϊ![]() ��
��

��1����������ߵĽ���ʽ��
��2����PΪx����һ�㣬����PAB���ܳ���Сʱ�������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����죬�����ɽ����������������������Դ�ḻ����Ȼ�������ξ�������ص㣮���������������������3Dħ������ij��������������ڶຣ�����οͣ���Ϊ������ʵ�����δ�������У�ij��ѧ���˽��У���꼶1200��ѧ����������Ȼ�������ξ�����˽�������Ӿţ�1�����ţ�2����ֱ��ȡ��30��ͬѧ���в��ԣ���������ǵijɼ����ٷ��ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
a�����Գɼ��ֳ�5�飬����A�飺50��x��60��B�飺60��x��70��C�飺70��x��80��D�飺80��x��90��E�飺90��x��100�����Գɼ�ͳ��ͼ���£�
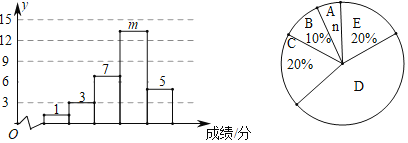
b���ţ�2����D��IJ��Գɼ��ֱ��ǣ�81��82��82��83��84��85��86��87��88��89��89��90��90��90��
c���ţ�1����2������Գɼ���ƽ��������λ�����������£�
�γ� | ƽ���� | ��λ�� | ���� |
�ţ�1�� | 84.2 | 84 | 89 |
�ţ�2�� | 84.6 | �� | 90 |
����������Ϣ���ش��������⣺
��1���������⣬ֱ��д��m��n��ֵ��m���� ����n���� �����ţ�2������Գɼ�����ͳ��ͼ��A���Բ�Ľ������� ������
��2���ڴ˴β����У�����Ϊ�� �����ѧ����������Ȼ���ľ�����˽⣨�����ţ�1���������ţ�2����������˵�����ɣ�һ�����ɼ��ɣ����� ����
��3�������У���꼶ѧ�����μӴ˴β��ԣ����Գɼ�����90��Ϊ���㣬����Ƹ�У���꼶��������Ȼ���ľ�����˽�ﵽ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B������ֱ�Ϊ��1��0������2��0���������κ���y=x2+��a��3��x+3��ͼ�����߶�ABֻ��һ�����㣬��a��ȡֵ��Χ��_______________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() .
.
��1���۲����
С�����֣���![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ����ͼ1��������
����ͼ1��������![]() �����
�����![]() ��
��![]() �����
�����![]() ֮����һ����������ϵ����ֱ��д�������ϵ��______��
֮����һ����������ϵ����ֱ��д�������ϵ��______��
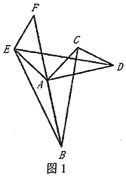
��2�����̽��
��ͼ2��![]() ��
��![]() ���е㣬��д��
���е㣬��д��![]() ��
��![]() ֮���������ϵ��λ�ù�ϵ����˵�����ɣ�
֮���������ϵ��λ�ù�ϵ����˵�����ɣ�
��3���������
��ͼ3��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���߶�
���߶�![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����ֱ��д��
����ֱ��д��![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A=90����AB=AC��BC=20��DE����ABC����λ�ߣ���M�DZ�BC��һ�㣬BM=3����N���߶�MC�ϵ�һ�����㣬����DN��ME��DN��ME�ཻ�ڵ�O������OMN��ֱ�������Σ���DO�ij���______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com