
【题目】如图,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .
.
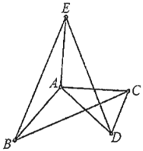
(1)观察猜想
小明发现,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图1,他发现
,如图1,他发现![]() 的面积
的面积![]() 与
与![]() 的面积
的面积![]() 之间有一定的数量关系,请直接写出这个关系:______;
之间有一定的数量关系,请直接写出这个关系:______;
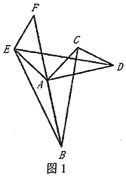
(2)类比探究
如图2,![]() 是
是![]() 的中点,请写出
的中点,请写出![]() 与
与![]() 之间的数量关系和位置关系,并说明理由;
之间的数量关系和位置关系,并说明理由;
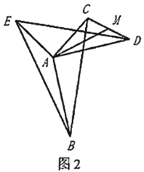
(3)解决问题
如图3,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在线段
在线段![]() 上,
上,![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
【答案】(1)![]() ;(2)BE=2AM,
;(2)BE=2AM,![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)结论:S1=S2.如图1中,作EH⊥BA交BA的延长线于H,CM⊥AD于M,利用三角形的面积公式证明即可;
(2)如图2中,延长![]() 至点
至点![]() 使得
使得![]() ,连接
,连接![]() ,易证
,易证![]() ,求出
,求出![]() ,然后证明
,然后证明![]() ,得到
,得到![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求出
,求出![]() 即可;
即可;
(3)作DT∥AC交AH的延长线于T.连接DE.证明△BAC≌△DAE(SAS),推出∠ADE=∠ABC=45°,BC=DE=2,推出∠BDE=∠BDA+∠ADE=90°,推出![]() ,再证明AH=
,再证明AH=![]() BE即可解决问题.
BE即可解决问题.
解:(1)结论:S1=S2.
理由:如图1中,作EH⊥BA交BA的延长线于H,CM⊥AD于M.
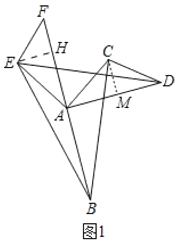
由题意CA=AE,AD=AB,∠CAE=∠DAF=90°,
∴∠EAH=∠CAM,
∴sin∠CAM=sin∠EAH,
∵S1=![]() ADCM=
ADCM=![]() ADACsin∠CAM,S2=
ADACsin∠CAM,S2=![]() ABEH=
ABEH=![]() ABAEsin∠EAH,
ABAEsin∠EAH,
∴S1=S2.
故答案为S1=S2;
(2)结论:BE=2AM,![]() ;
;
理由:延长![]() 至点
至点![]() 使得
使得![]() ,连接
,连接![]() ,
,
易证![]() ,
,
∴![]() 且
且![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
延长![]() 交
交![]() 于点
于点![]() ,
,
在![]() 中,
中,![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ;
;
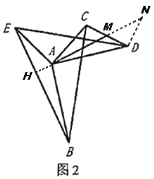
(3)作DT∥AC交AH的延长线于T,连接DE.
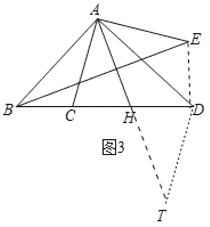
∵AB=AD,AC=AE,∠BAD=∠CAE=90°,
∴∠ABD=∠ADB=45°,∠BAC=∠DAE,
∴△BAC≌△DAE(SAS),
∴∠ADE=∠ABC=45°,BC=DE=2,
∴∠BDE=∠BDA+∠ADE=90°,
∴BE=![]() ,
,
∵∠BAD=∠CAE=90°,
∴∠CAD+∠BAE=180°,
∵AC∥DT,
∴∠CAD+∠ADT=180°,
∴∠BAE=∠ADT,
∵AH⊥BE,
∴∠DAT+∠BAT=90°,∠ABE+∠BAT=90°,
∴∠DAT=∠ABE,
∵AB=AD,
∴△ABE≌△DAT(ASA),
∴BE=AT,AE=DT,
∵AC=AE,
∴AC=DT,
∵∠CAH=∠T,∠AHC=∠DHT,
∴△AHC≌△THD(AAS),
∴AH=HT,
∴AH=![]() BE=
BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游客乘坐“金碧皇宫号游船”在长江和嘉陵江的交汇处A点,测得来福土最高楼顶点F的仰角为45°,此时他头项正上方146米的点B处有架航拍无人机测得来福士最高楼顶点F的仰角为31°,游船朝码头方向行驶120米到达码头C,沿坡度i=1:2的斜坡CD走到点D,再向前走160米到达来福士楼底E,则来福士最高楼EF的高度约为( )(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.87,tan31°≈0.60)
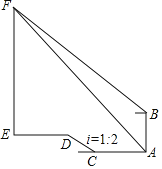
A.301.3米B.322.5米C.350.2米D.418.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
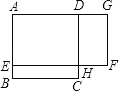
【题目】如图,ABCD是一块边长为8米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在A的延长线上,DG=2BE,设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
(1)求y与x之间的函数关系式(不需写自变量的取值范围);
(2)若改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,此时BE的长为 米.
(3)当x为何值时改造后的矩形苗圃AEFG的最大面积?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,F是半圆弧AB的中点,E是弧BF上一点,直线AE与过点B的切线相交于点C,连接EF.
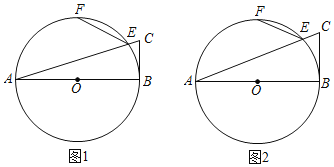
(1)若EF=![]() AB,求∠ACB的度数;
AB,求∠ACB的度数;
(2)若⊙O的半径为3,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
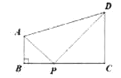
【题目】如图,四边形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=3,点P为BC边上一动点,若△PAB与△PCD是相似三角形,则BP的长为 _____________
查看答案和解析>>
科目:初中数学 来源: 题型:
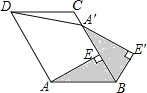
【题目】如图,已知平行四边形ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的度数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com