
【题目】如图,在⊙O中,AB为直径,F是半圆弧AB的中点,E是弧BF上一点,直线AE与过点B的切线相交于点C,连接EF.
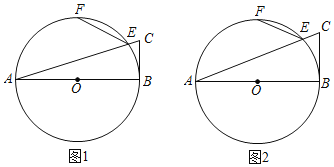
(1)若EF=![]() AB,求∠ACB的度数;
AB,求∠ACB的度数;
(2)若⊙O的半径为3,BC=2,求EF的长.
【答案】(1)75°;(2)![]()
【解析】
(1)连接OE、OF、AF,根据等边三角形的性质得到∠EOF=60°,由圆周角定理得到∠EAF=![]() ∠EOF=30°,根据切线的性质得到∠ABC=90°,根据直角三角形的性质计算即可;
∠EOF=30°,根据切线的性质得到∠ABC=90°,根据直角三角形的性质计算即可;
(2)连BE、AF、BF,过F作FM⊥EF交AE于M,根据勾股定理求出AC,根据三角形的面积公式求出BE,证明△AFM≌△BFE,根据全等三角形的性质得到AM=BE,EF=FM,根据等腰直角三角形的性质计算,得到答案.
解:(1)连接OE、OF、AF,
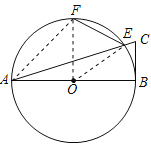
∵EF=![]() AB=OE=OF,
AB=OE=OF,
∴△EOF为等边三角形,
∴∠EOF=60°,
由圆周角定理得,∠EAF=![]() ∠EOF=30°,
∠EOF=30°,
∵F是半圆弧AB的中点,
∴∠AOF=90°,
∴∠OAF=45°,
∴∠CAB=15°,
∵BC为⊙O的切线,
∴∠ABC=90°,
∴∠ACB=75°;
(2)连BE、AF、BF,过F作FM⊥EF交AE于M,
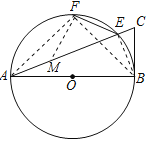
则∠AEB=∠CEB=90°.
∵∠ABC=90°,AB=6,BC=2,
∴AC=![]() =
=![]() =2
=2![]() ,
,
由面积法得,BE=![]() =
=![]() ,
,
∴AE=![]() =
=![]() ,
,
∵AB为直径,
∴∠AFB=90°,又FM⊥EF,
∴∠AFM=∠BFE,
在△AFM和△BFE中,
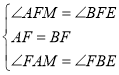 ,
,
∴△AFM≌△BFE(ASA),
∴AM=BE=![]() ,EF=FM.
,EF=FM.
∵EM=AE﹣AM=![]() ,
,
∴EF=![]() EM=
EM=![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
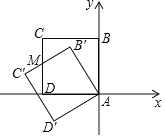
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则M的坐标为( )
A.(1,![]() )B.(﹣1,
)B.(﹣1,![]() )C.(1,
)C.(1,![]() )D.(﹣1,
)D.(﹣1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆,别称“山城”、“雾都”,旅游资源丰富,自然人文旅游景点独具特点.近年来,重庆以其独特“3D魔幻”般的城市魅力吸引了众多海内外游客,成为名副其实的旅游打卡网红城市.某中学想了解该校九年级1200名学生对重庆自然人文旅游景点的了解情况,从九(1)、九(2)班分别抽取了30名同学进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:
a.测试成绩分成5组,其中A组:50<x≤60,B组:60<x≤70,C组:70<x≤80,D组:80<x≤90,E组:90<x≤100.测试成绩统计图如下:
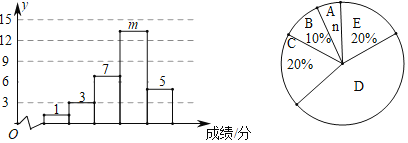
b.九(2)班D组的测试成绩分别是:81、82、82、83、84、85、86、87、88、89、89、90、90、90.
c.九(1)(2)班测试成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
九(1) | 84.2 | 84 | 89 |
九(2) | 84.6 | π | 90 |
根据以上信息,回答下列问题:
(1)根据题意,直接写出m,n的值:m= ,n= ;九(2)班测试成绩扇形统计图中A组的圆心角α= °;
(2)在此次测试中,你认为 班的学生对重庆自然人文景点更了解(填“九(1)”或“九(2)”),请说明理由(一条理由即可): ;
(3)假设该校九年级学生都参加此次测试,测试成绩大于90分为优秀,请估计该校九年级对重庆自然人文景点的了解达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
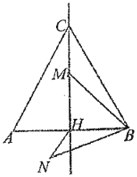
【题目】如图,等边三角形![]() 的边长是2,
的边长是2,![]() 是高
是高![]() 所在直线上的一个动点,连接
所在直线上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,则在点
,则在点![]() 运动过程中,线段
运动过程中,线段![]() 长度的最小值是( )
长度的最小值是( )
A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .
.
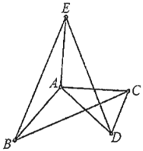
(1)观察猜想
小明发现,将![]() 绕点
绕点![]() 逆时针旋转
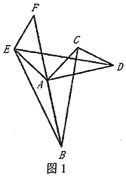
逆时针旋转![]() ,如图1,他发现
,如图1,他发现![]() 的面积
的面积![]() 与
与![]() 的面积
的面积![]() 之间有一定的数量关系,请直接写出这个关系:______;
之间有一定的数量关系,请直接写出这个关系:______;
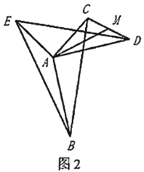
(2)类比探究
如图2,![]() 是
是![]() 的中点,请写出
的中点,请写出![]() 与
与![]() 之间的数量关系和位置关系,并说明理由;
之间的数量关系和位置关系,并说明理由;
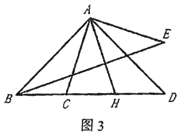
(3)解决问题
如图3,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在线段
在线段![]() 上,
上,![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
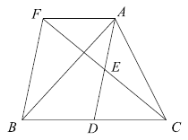
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的一点,连接
边上的一点,连接![]() ,
,![]() 是
是![]() 边上的中点,过点
边上的中点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)如果![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3经过点A(﹣1,0),B(3,0),与y轴交于点C.点D(xD,yD)为抛物线上一个动点,其中1<xD<3.连接AC,BC,DB,DC.
(1)求该抛物线的解析式;
(2)当△BCD的面积等于△AOC的面积的2倍时,求点D的坐标;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com