
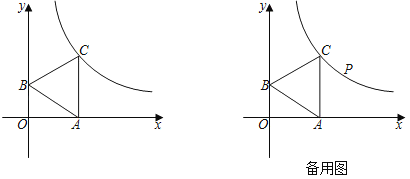
【题目】如图,点A、B分别在x轴和y轴的正半轴上,以线段AB为边在第一象限作等边△ABC,![]() ,且CA∥y轴.
,且CA∥y轴.
(1)若点C在反比例函数![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)在(1)中的反比例函数图象上是否存在点N,使四边形ABCN是菱形,若存在请求出点N坐标,若不存在,请说明理由.
(3)点P在第一象限的反比例函数图象上,当四边形OAPB的面积最小时,求出P点坐标.
【答案】(1)y=![]() ;(2)存在,N(2
;(2)存在,N(2![]() ,1);(3)P(
,1);(3)P(![]() ,
,![]() ).
).
【解析】
(1)如图1中,作CD⊥y轴于D.首先证明四边形OACD是矩形,利用反比例函数k的几何意义解决问题即可.
(2)如图2中,作BD⊥AC于D,交反比例函数图象于N,连接CN,AN.求出![]() 的坐标,证明四边形ABCN是菱形即可.
的坐标,证明四边形ABCN是菱形即可.
(3)如图3中,连接PB,PA,OP.设P(a,![]() ).可得S四边形OAPB=S△POB+S△POA=
).可得S四边形OAPB=S△POB+S△POA=![]() ×1×a+
×1×a+![]() ×
×![]() ×
×![]() =
=![]() a+
a+![]() =
=![]() 由此即可解决问题.
由此即可解决问题.
解:(1)如图1中,作CD⊥y轴于D.

∵CA∥y轴,CD⊥y轴,
∴CD∥OA,AC∥OD,
∴四边形OACD是平行四边形,
∵∠AOD=90°,
∴四边形OACD是矩形,
∴k=S矩形OACD=2S△ABC=![]() ,
,
∴反比例函数的解析式为y=![]() .
.
(2)如图2中,作BD⊥AC于D,交反比例函数图象于N,连接CN,AN.

∵△ABC是等边三角形,面积为![]() ,设CD=AD=m,则BD=
,设CD=AD=m,则BD=![]() m,
m,
∴![]() ×2m×
×2m×![]() m=
m=![]() ,
,
∴m=1或﹣1(舍弃),
∴B(0,1),C(![]() ,2),A(
,2),A(![]() ,0),
,0),
∴N(2![]() ,1),
,1),
∴BD=DN,
∵AC⊥BN,
∴CB=CN,AB=AN,
∵AB=BC,
∴AB=BC=CN=AN,
∴四边形ABCN是菱形,
∴N(2![]() ,1).
,1).
(3)如图3中,连接PB,PA,OP.设P(a,![]() ).
).

S四边形OAPB=S△POB+S△POA=![]() ×1×a+
×1×a+![]() ×
×![]() ×
×![]() =
=![]() a+
a+![]() =
=![]()
∴当![]() a=
a=![]() 时,四边形OAPB的面积最小,
时,四边形OAPB的面积最小,
解得a=![]() 或
或![]() (舍弃),
(舍弃),
此时P(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
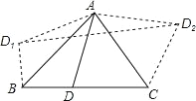
【题目】如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
+2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班![]() 名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
金额/元 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 18 | 10 | 8 | 2 |
A.平均数为![]() 元B.众数为
元B.众数为![]() 元C.中位数为
元C.中位数为![]() 元D.极差为
元D.极差为![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
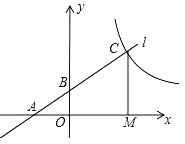
【题目】已知:如图,直线l经过点A(﹣2,0)和点B(0,1),点M在x轴上,过点M作x轴的垂线交直线l于点C,若OM=2OA,则经过点C的反比例函数表达式为( )
A.y=![]() B.y=
B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了解同学们对金庸武侠小说的阅读情况,随机对初三年级的部分同学进行调查,将调查结果分成以下五类:A:看过0~3本,B:看过4~6本,C:看过7~9本,D:看过10~12本,E:看过13~15本.并根据调查结果绘制了如图1、图2两幅不完整的统计图.
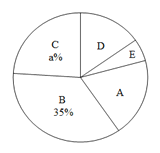
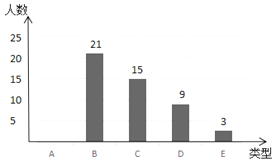
(1)图2中的a = ,D所对的圆心角度数为 °;
(2)请补全条形统计图;
(3)本次调查中E类有2男1女,王老师想从中抽取2名同学分别撰写一篇读书笔记.请用列表或画树状图的方法求所抽取的两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第24届冬奥会将于2022年在北京和张家口举行,冬奥会的项目有滑雪(如高山滑雪、单板滑雪等),滑冰(如速度滑冰、花样滑冰等),冰球,冰壶等.如图,有4张形状、大小、质地均相同的卡片,正面分别印有单板滑雪、速度滑冰、冰球、冰壶4种不同的图案,背面完全相同.现将这4张卡片洗匀后正面向下放在桌子上.

(1)从中随机抽取1张,抽出的卡片上恰好是滑雪项目图案的概率是 .
(2)若印有单板滑雪、速度滑冰、冰球、冰壶4种不同图案的卡片分别用A,B,C,D表示,从中随机抽取两张,试用画树状图或列表的方法求出印有冰球图案的卡片被抽中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:当点P在射线OA上时,把![]() 的的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.
的的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.
例如:如图1,△OAB三个顶点均在格点上,BP是OA边上的高,则点P和点B在射线OA上的射影值均为![]() =
=![]() .
.

(1)在△OAB中,
①点B在射线OA上的射影值小于1时,则△OAB是锐角三角形;
②点B在射线OA上的射影值等于1时,则△OAB是直角三角形;
③点B在射线OA上的射影值大于1时,则△OAB是钝角三角形.
其中真命题有 .
A.①②B.①③C.②③D.①②③
(2)已知:点C是射线OA上一点,CA=OA=1,以〇为圆心,OA为半径画圆,点B是⊙O上任意点.
①如图2,若点B在射线OA上的射影值为![]() .求证:直线BC是⊙O的切线;
.求证:直线BC是⊙O的切线;
②如图3,已知D为线段BC的中点,设点D在射线OA上的射影值为x,点D在射线OB上的射影值为y,直接写出y与x之间的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,H是对角线BD的中点,延长DC至E,使得DE=DB,连接BE,作DF⊥BE交BC于点G,交BE于点F,连接CH、FH,下列结论:(1)HC=HF;(2)DG=2EF;(3)BE·DF=2CD2;(4)S△BDE=4S△DFH;(5)HF∥DE,正确的个数是( )

A.5B.4C.3D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com