Question

【题目】如图，P为正方形ABCD内一点，PA=1，PB=2，PC=3．

（1）将△ABP绕点B顺时针旋转90°，得到△BEC，请你画出△BEC．

（2）连接PE，求证：△PEC是直角三角形；

（3）填空：∠APB的度数为 ．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）135°．

【解析】

试题分析：（1）将△APB绕B点顺时针旋转90°，即将A，P，两点绕B点顺时针旋转90°，得出△CBE即可；（2）根据旋转的性质，得出∠PBE=∠ABC=90°，BP=BE=2，即可证得△PBE是等腰直角三角形，从而求得PE，最后根据勾股定理的逆定理，即可得到△PEC是直角三角形；（3）连接PE后，存在两个直角三角形：Rt△PBE和Rt△PCE，先求得∠BEC的度数，最后根据全等三角形的对应角相等，即可得出∠APB的度数．

试题解析：（1）如图所示，△CBE即为所求；

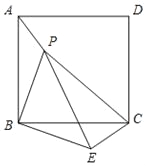
（2）证明：∵△BEC是由△APB绕点B顺时针方向旋转90°得到的，

∴△BEC≌△BPA，∠PBE=90°，

∴BE=BP=2，CE=PA=1，

∴△PBE是等腰直角三角形，CE2=1，

∴Rt△PBE中，PE2=PB2+BE2=4+4=8，

又∵PC=3，

∴PC2=9，

∴在△PCE中，PE2+CE2=PC2，

∴△PCE是直角三角形，且∠PEC=90°；

（3）由（2）可得，△PCE是直角三角形，△PBE是等腰直角三角形，

∴∠PEC=90°，∠BEP=45°，

∴∠BEC=90°+45°=135°，

又∵△BEC≌△BPA，

∴∠APB=∠BEC=135°．