
 如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB•CF;③CF=FD;④△ABE∽△AEF.其中正确的有( )
如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB•CF;③CF=FD;④△ABE∽△AEF.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由正方形的性质和三角函数得出∠BAE<30°,①不正确;由题中条件可得△CEF∽△BAE,进而得出对应线段成比例,得出②正确,CF=$\frac{1}{3}$FD,③不正确;进而又可得出△ABE∽△AEF,得出④正确,即可得出题中结论.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CAD,∠B=∠C=∠D=90°,
∵E是BC的中点,
∴BE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$AB,
∵AE>AB,
∴sin∠BAE=$\frac{BE}{AE}$<$\frac{1}{2}$,
∴∠BAE<30°,①不正确;
∵AE⊥EF,∴∠BAE=∠CEF,
∴△CEF∽△BAE,
∴$\frac{CE}{AB}=\frac{CF}{BE}$=$\frac{CF}{BE}$=$\frac{1}{2}$,
∴CE•BE=AB•CF,CF=$\frac{1}{2}$BE=$\frac{1}{4}$CD,
∵BE=CE,CF=$\frac{1}{3}$FD,
∴CE2=AB•CF,②正确,③不正确;
由△CEF∽△BAE可得$\frac{CE}{CF}=\frac{AB}{BE}$,
∴∠EAF=∠BAE的正切值相同,
∴∠EAF=∠BAE,
又∠B=∠C=90°.
∴△ABE∽△AEF,
∴④正确;
正确的有2个,
故选:B.
点评 本题主要考查了正方形的性质、相似三角形的判定及性质、三角函数;熟练掌握正方形的性质,证明三角形相似是解决问题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面内有公共端点的四条射线OA,OB,OC,OD,从射线OA开始按逆时针方向依次在射线上写出数字2,-4,6,-8,10,-12,….则第16个数应是-32;“-2016”在射线OD上.
如图,平面内有公共端点的四条射线OA,OB,OC,OD,从射线OA开始按逆时针方向依次在射线上写出数字2,-4,6,-8,10,-12,….则第16个数应是-32;“-2016”在射线OD上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:函数y=ax2+bx+c的图象交x轴于点B,C,交y轴于点A.
如图:函数y=ax2+bx+c的图象交x轴于点B,C,交y轴于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
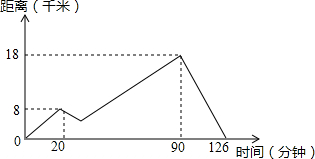 如图表示一条船从点A到河的上游点B往返的情形,从A点出发20分钟后,发动机坏了一段时间,船顺着河水倒着走了一段,之后发动机修好,继读前进到达,接着立即向点A返回.假设河水的流速、船行驶时在静水中的速度是不变的,这艘船在静水中的速度是多少?
如图表示一条船从点A到河的上游点B往返的情形,从A点出发20分钟后,发动机坏了一段时间,船顺着河水倒着走了一段,之后发动机修好,继读前进到达,接着立即向点A返回.假设河水的流速、船行驶时在静水中的速度是不变的,这艘船在静水中的速度是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com