
【题目】外线投篮是篮球队常规训练的重要项目之一,下列图表中数据是甲、乙、丙三人每人十次投篮测试的成绩.测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
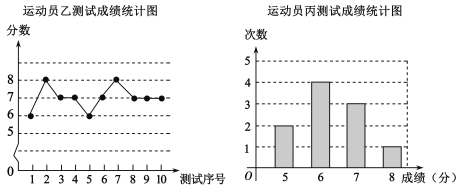
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三人中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①对角线互相垂直的四边形是菱形;②若![]() ,则
,则![]() ;③两个位似图形一定是相似图形;④若
;③两个位似图形一定是相似图形;④若![]() ,则
,则![]() ;其中原命题是真命题逆命题是假命题的有( )
;其中原命题是真命题逆命题是假命题的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形![]() 中,线段
中,线段![]() 绕矩形外一点
绕矩形外一点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,使
,使![]() 点的对应点
点的对应点![]() 落在射线
落在射线![]() 上,
上,![]() 点的对应点
点的对应点![]() 在
在![]() 的延长线上.
的延长线上.
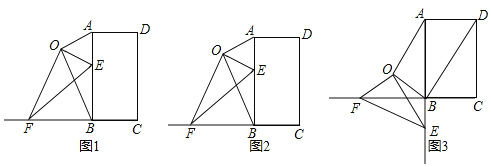
(1)如图1,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 与
与![]() 的大小关系为______________.
的大小关系为______________.
(2)如图2,当点![]() 位于线段
位于线段![]() 上时,求证:
上时,求证:![]() ;
;
(3)如图3,当点![]() 位于线段
位于线段![]() 的延长线上时,
的延长线上时,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市精准扶贫工作已经进入攻坚阶段,贫困的张大爷在某单位的帮扶下,把一片坡地改造后种植了大樱桃.今年正式上市销售,在销售30天中,第一天卖出20千克,为了扩大销量,在一段时间内采取降价措施,每天比前一天多卖出4千克.当售价不变时,销售量也不发生变化.已知种植销售大樱桃的成本为18元/千克,设第![]() 天的销售价
天的销售价![]() 元/千克,
元/千克,![]() 与
与![]() 函数关系如下表:
函数关系如下表:
表一
天数 | 1 | 2 | 3 | …… | …… | 20 |
售价(元/千克) | 37.5 | 37 | 36.5 | …… | …… | 28 |
表二
天数 | 21 | 22 | …… | …… | 30 |
售价(元/千克) | 28 | 28 | …… | …… | 28 |
(1)求![]() 与
与![]() 函数解析式;
函数解析式;
(2)求销售大樱桃第几天时,当天的利润最大?最大利润是多少?
(3)销售大樱桃的30天中,当天利润不低于
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,以
中,以![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 于点
于点![]() ,
,![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,交
,交![]() 于点
于点![]() .
.
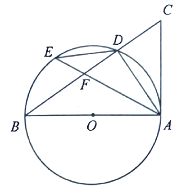
(1)若![]() ,求证:
,求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
(3)在(2)的条件下,若![]() ,求⊙
,求⊙![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD中,AB=5,∠B=60°,⊙A的半径为2,⊙B的半径为3,点E、F分别为⊙A、⊙B上的动点,点P为DC边上的动点,则PE+PF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级: 79,85,73,80, 75,76,87, 70, 75,94,75,79,81,71, 75,80,86,59, 83, 77.
八年级: 92,74, 87,82,72,81, 94,83,77, 83,80,81,71,81,72,77,82,80,70,41.
整理数据:

分析数据:

应用数据:
(1)由上表填空: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com