已知等腰三角形的两边长分别为6和5.则这个等腰三角形的周长是( ) A.15或16B.16C.17D.16或17 题目和参考答案——青夏教育精英家教网—

已知等腰三角形的两边长分别为6和5，则这个等腰三角形的周长是（　　）

A、15或16	B、16
C、17	D、16或17

考点：等腰三角形的性质,三角形三边关系

专题：

分析：分6是腰长和底边两种情况，利用三角形的三边关系判断，然后根据三角形的周长的定义列式计算即可得解．

解答：解：①6是腰长时，三角形的三边分别为6、6、5，
能组成三角形，
周长=6+6+5=17，
②6是底边时，三角形的三边分别为6、5、5，
能组成三角形，
周长=6+5+5=16，
综上所述，三角形的周长为16或17．
故选D．

点评：本题考查了等腰三角形的性质，三角形的三边关系，难点在于分情况讨论．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

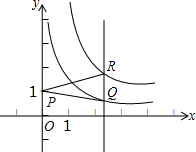函数y=

（x＞0）与y=

（x＞0）的图象如图所示，点P是y轴上的任意一点，直线x=t（t＞0）分别与两个函数图象交于点Q，R，连接PQ，PR．
（1）用t表示PQ的长度，并判断随着t的值逐渐增大，RQ长度的变化情况；
（2）当t从小到大变化时，△PQR的面积是否发生变化？请说明理由；
（3）当t=1时，△PQR的周长是否发生变化？如果发生变化，当P点坐标为

时，△PQR的周长最小，最小周长是

；如果不发生变化，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

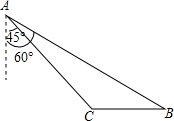如图，到海岛景区C有两条旅游线路可供选择，游人可从码头A乘游艇或从码头B乘游船前往，已知B在A南偏东60°方向，C位于A南偏东45°方向10海里处，且C在B正西方向，游艇的速度为每小时30海里，游船的速度为每小时13海里，问游客选择哪条线路用时较少？并说明理由．（参考数据：

≈1.41，

≈1.73，

≈2.45）

查看答案和解析>>

科目：初中数学 来源： 题型：

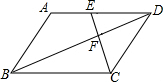如图，在平行四边形ABCD中，点E是边AD上的一点，且AE：ED=2：3，EC交对角线BD于点F，则EF：FC等于（　　）

A、3：2	B、2：5
C、2：3	D、3：5

查看答案和解析>>

科目：初中数学 来源： 题型：

课堂上，老师提出这样一个问题：你能用手中的矩形纸片尽可能大的折出一个菱形吗？有两位同学很快折出了各自不同的菱形，如下图：
（1）如果该矩形纸片的长为4，宽为3，则图1、图2两图中的菱形面积分别为：

；

；
（2）这时老师说，这两位同学折出的菱形都不是最大的，聪明的你能够想出最大的菱形应该怎样折出来吗？如图3所示：在矩形ABCD中，设AB=3，AD=4，请你在图中画出面积最大的菱形的示意图，标注上适当的字母，并求出这个菱形的面积．
（3）借题发挥：如图4，在矩形ABCD中，AB=2，AD=3，若折叠该矩形，使得点D与AB边的中点E重合，折痕交AD于点F，交BC于点G，边DC折叠后与BC交于点M，试求：△EBM的面积．